《2025年名校题库七年级数学上册》

4. (双流区期末)幻方最早起源于中国,在《自然科学大事年表》中,对幻方做了特别的述说：“公元前一世纪,《大戴礼》记载,中国古代有象征吉祥的河图、洛书、纵横图,即为九宫算,被认为是现代组合数学最古老的发现。”请将$-4$,$-3$,$-2$,$-1$,$0$,$1$,$2$,$3$,$4$分别填入如图所示的幻方中,要求同一横行、同一竖行以及同一条斜对角线上的三个数相加都得$0$,则$x+y$的值为______。

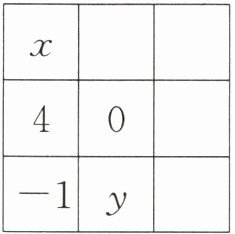
答案：
-5 [解析]如图所示,由题意，知$4+0+c=0$，$x+4+(-1)=0$，$-1+0+b=0$，$x+a+b=0$，$a+0+y=0$，解得$c=-4$，$x=-3$，$b=1$，$a=2$，$y=-2$，$\therefore x+y=-3+(-2)=-5$。
　　　　　　

5. (成华区期末)幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”,把洛书用今天的数学符号翻译出来,就是一个三阶幻方。如图1,将9个数填在$3×3$(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方。在如图2所示的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则$m= $______,$n= $______。

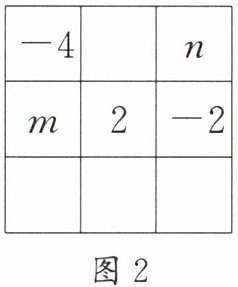
答案： 6 0 [解析]由题意,知$-4+2=n+(-2)$，解得$n=0$。又$-4+m=n+2$，即$-4+m=2$，解得$m=6$。

6. (七中万达)规定：$f(x)= |x-2|$,$g(y)= |y+4|$,例如$f(4)= |4-2|= 2$,$g(-3)= |-3+4|= 1$。下列结论中,正确的是______。(填序号)
①式子$f(x-1)+g(x+1)的最小值是8$；
②若$f(x)+g(y)= 0$,则$2x+y= 0$；
③能使$f(x)= g(x)成立的x$的值不存在；
④若$x\leqslant -4$,则$f(x)-g(x)$为定值。

答案： ①②④ [解析]$\because f(x-1)=|x-1-2|=|x-3|$，$g(x+1)=|x+1+4|=|x+5|$，$\therefore f(x-1)+g(x+1)=|x-3|+|x+5|$。$\because |x-3|+|x+5|$的几何意义是数轴上表示数$x$的点分别到表示数 3 和$-5$的两个点的距离之和，$\therefore |x-3|+|x+5|$的最小值为 8，故①正确。$\because f(x)+g(y)=|x-2|+|y+4|=0$，$\therefore \begin{cases} x-2=0 \\ y+4=0 \end{cases}$，解得$\begin{cases} x=2 \\ y=-4 \end{cases}$，$\therefore 2x+y=2×2-4=0$，故②正确。$\because f(x)=g(x)$，$\therefore |x-2|=|x+4|$，$\therefore x-2=x+4$或$x-2=-(x+4)$，解得$x=-1$，故③不正确。④当$x \leq -4$时，$f(x)-g(x)=|x-2|-|x+4|=-(x-2)-[-(x+4)]=6$，故④正确。综上所述，正确的是①②④。

7. (石室联中)同学们都熟悉“幻方”游戏,现将“幻方”游戏稍作改进变成“幻圆”游戏,将$-6$,$8$,$-10$,$12$,$-14$,$16$,$-18$,$20$分别填入图中的圆圈内,使横、竖以及内外两个圈上$4$个数之和都相等,则$a+b$的值为______。

答案：
-28 或 10 [解析]如图，$\because -6+8-10+12 -14+16-18+20=8$，$\therefore$横、竖以及内外两个圈上$4$个数之和都相等，$\therefore -14+12+16+a=4$，$\therefore a=-10$。$\because 12+8+a+c=4$，$b+16-14+d=4$，$\therefore c=-6$，$b+d=2$，$\therefore b=-18$或$b=20$。当$b=-18$时，$d=20$，此时$a+b=-10-18=-28$；当$b=20$时，$d =-18$，此时$a+b=-10+20=10$。$\therefore a+b$的值为$-28$或$10$。
　　　　　　

8. (郫都区期末)设$x$,$y$是任意两个有理数,规定$x与y$之间的一种运算“$\oplus$”为：$x\oplus y= \begin{cases}3x+4y-5(x\geqslant y),\\4x+3y-5(x\lt y)。\end{cases} $
(1)求$1\oplus(-1)$的值；
(2)若$(m-2)\oplus(m+3)= 2$,求$m$的值。

答案： 解：
(1)$1\oplus(-1)=3×1+4×(-1)-5=-6$；
(2)显然$m-2 ＜ m+3$，所以$(m-2)\oplus(m+3)=4(m-2)+3(m+3)-5=2$，解得$m=\frac{6}{7}$。