第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. (锦江区期末)如图,数轴上$A$,$B两点对应的数分别是a$,$b$,且$(a + 4)^2+\vert b - 12\vert = 0$.
(1)$a = $______,$b = $______.
(2)点$M从点A$出发沿数轴正方向匀速运动,同时,点$N从点B$出发沿数轴负方向匀速运动,设运动时间为$t$秒.$P$,$Q分别为AM$,$BN$的中点,规定:若$MN = kPQ$($k$为常数),则称点$P$,$Q为点M$,$N$的“$k$型伴点”.
①若点$M的运动速度为每秒2$个单位长度,点$N的运动速度为每秒3$个单位长度,当点$P$,$Q为点M$,$N$的“$2$型伴点”时,求$t$的值;
②若点$N$保持①中的速度不变,改变点$M$的速度,当点$P$,$Q为点M$,$N$的“$3$型伴点”时,点$P刚好运动到线段AB$的中点处,则点$M$的速度应变为多少?
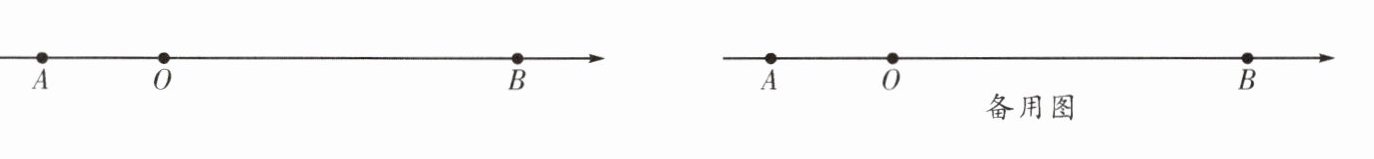
(1)$a = $______,$b = $______.
(2)点$M从点A$出发沿数轴正方向匀速运动,同时,点$N从点B$出发沿数轴负方向匀速运动,设运动时间为$t$秒.$P$,$Q分别为AM$,$BN$的中点,规定:若$MN = kPQ$($k$为常数),则称点$P$,$Q为点M$,$N$的“$k$型伴点”.
①若点$M的运动速度为每秒2$个单位长度,点$N的运动速度为每秒3$个单位长度,当点$P$,$Q为点M$,$N$的“$2$型伴点”时,求$t$的值;
②若点$N$保持①中的速度不变,改变点$M$的速度,当点$P$,$Q为点M$,$N$的“$3$型伴点”时,点$P刚好运动到线段AB$的中点处,则点$M$的速度应变为多少?
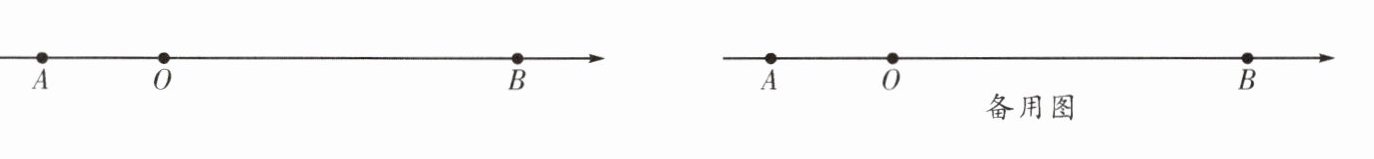
答案:
(1)-4;12
(2)解:①由题意得,数轴上点M对应的数为$-4 + 2t$,点N对应的数为$12 - 3t$.$\because$P,Q分别为AM,BN的中点,$\therefore$数轴上点P对应的数为$-4 + t$,点Q对应的数为$12 - \frac{3}{2}t$.$\because$点P,Q为点M,N的“2型伴点”,$\therefore MN = 2PQ$,即$|(-4 + 2t) - (12 - 3t)| = 2|(-4 + t) - (12 - \frac{3}{2}t)|$,整理得$|5t - 16| = |5t - 32|$,即$5t - 16 = 5t - 32$(无解)或$5t - 16 = 32 - 5t$,解得$t = \frac{24}{5}$. ②设点M的速度为a个单位长度/秒,当点P刚好运动到线段AB的中点处时,点M此时与点B重合,$\therefore$点P对应的数为$-4 + \frac{1}{2}at = 4$,点M对应的数为12.$\because$点P,Q为点M,N的“3型伴点”,$\therefore |12 - (12 - 3t)| = 3|4 - (12 - \frac{3}{2}t)|$,整理得$|3t| = |-24 + \frac{9}{2}t|$,即$3t = - 24 + \frac{9}{2}t$或$3t = 24 - \frac{9}{2}t$,解得$t = 16$或$t = \frac{16}{5}$.当$t = 16$时,$-4 + 8a = 4$,解得$a = 1$;当$t = \frac{16}{5}$时,$-4 + \frac{8}{5}a = 4$,解得$a = 5$.综上所述,点M的速度应变为1个单位长度/秒或5个单位长度/秒.
(1)-4;12
(2)解:①由题意得,数轴上点M对应的数为$-4 + 2t$,点N对应的数为$12 - 3t$.$\because$P,Q分别为AM,BN的中点,$\therefore$数轴上点P对应的数为$-4 + t$,点Q对应的数为$12 - \frac{3}{2}t$.$\because$点P,Q为点M,N的“2型伴点”,$\therefore MN = 2PQ$,即$|(-4 + 2t) - (12 - 3t)| = 2|(-4 + t) - (12 - \frac{3}{2}t)|$,整理得$|5t - 16| = |5t - 32|$,即$5t - 16 = 5t - 32$(无解)或$5t - 16 = 32 - 5t$,解得$t = \frac{24}{5}$. ②设点M的速度为a个单位长度/秒,当点P刚好运动到线段AB的中点处时,点M此时与点B重合,$\therefore$点P对应的数为$-4 + \frac{1}{2}at = 4$,点M对应的数为12.$\because$点P,Q为点M,N的“3型伴点”,$\therefore |12 - (12 - 3t)| = 3|4 - (12 - \frac{3}{2}t)|$,整理得$|3t| = |-24 + \frac{9}{2}t|$,即$3t = - 24 + \frac{9}{2}t$或$3t = 24 - \frac{9}{2}t$,解得$t = 16$或$t = \frac{16}{5}$.当$t = 16$时,$-4 + 8a = 4$,解得$a = 1$;当$t = \frac{16}{5}$时,$-4 + \frac{8}{5}a = 4$,解得$a = 5$.综上所述,点M的速度应变为1个单位长度/秒或5个单位长度/秒.
查看更多完整答案,请扫码查看


