《2025年名校题库七年级数学上册》

1. (成华区期末)已知整数$a_{1},a_{2},a_{3},a_{4}$满足下列条件：$a_{1}= 0,a_{2}= -|a_{1}+1|,a_{3}= -|a_{2}+2|,a_{4}= -|a_{3}+3|$,以此类推,则$a_{2021}$的值为____.

答案： -1010 【解析】由题意可得，a₁=0，a₂=-|a₁+1|=-1，a₃=-|a₂+2|=-1，a₄=-|a₃+3|=-2，a₅=-|a₄+4|=-2，……，
∴a₂₀₂₁=-$\frac{2021-1}{2}$=-1010.

2. (西川)一列数$a_{1},a_{2},a_{3},a_{4},... $满足条件：$a_{1}= \frac {1}{2},a_{n}= \frac {1}{1-a_{n-1}}(n≥2$,且n为正整数),则$a_{2016}= $____.

答案： -1 【解析】
∵a₁=$\frac{1}{2}$，a₂=$\frac{1}{1-\frac{1}{2}}$=2，a₃=$\frac{1}{1-2}$=-1，a₄=$\frac{1}{1+1}$=$\frac{1}{2}$，
∴每三个数一循环.
∵2016÷3=672，
∴a₂₀₁₆=a₃=-1.

3. (成华区期末)已知$a_{1}= \frac {1}{2},a_{2}= -a_{1}-1,a_{3}= \frac {1}{a_{2}},a_{4}= -a_{3}-1,a_{5}= \frac {1}{a_{4}},... $(即当n为大于1的奇数时,$a_{n}= \frac {1}{a_{n-1}}$;当n为大于1的偶数时,$a_{n}= -a_{n-1}-1$),按此规律,$a_{2022}= $____.

答案： 2 【解析】当a₁=$\frac{1}{2}$时，a₂=-$\frac{1}{2}$-1=-$\frac{3}{2}$，a₃=$\frac{1}{-\frac{3}{2}}$=-$\frac{2}{3}$，a₄=-(-$\frac{2}{3}$)-1=-$\frac{1}{3}$，a₅=$\frac{1}{-\frac{1}{3}}$=-3，a₆=-(-3)-1=2，a₇=$\frac{1}{2}$，……，
∴由此可得所得的数列每6个一循环.
∵2022÷6=337，
∴a₂₀₂₂=a₆=2.

4. (成华区期末)观察按一定规律排列的一组数：$2,\frac {1}{2},\frac {2}{7},... $,其中第n个数记为$a_{n}$,第$n+1个数记为a_{n+1}$,第$n+2个数记为a_{n+2}$,且满足$\frac {1}{a_{n}}+\frac {1}{a_{n+2}}= \frac {2}{a_{n+1}}$,则$a_{4}= $____,$a_{2023}= $____.

答案： $\frac{1}{5}$ $\frac{2}{6067}$ 【解析】由题意，得a₁=2，a₂=$\frac{1}{2}$，a₃=$\frac{2}{7}$.
∵$\frac{1}{a_n}$+$\frac{1}{a_{n+2}}$=$\frac{2}{a_{n+1}}$，
∴当n=2时，$\frac{1}{a_2}$+$\frac{1}{a_4}$=$\frac{2}{a_3}$，即$\frac{1}{\frac{1}{2}}$+$\frac{1}{a_4}$=$\frac{2}{\frac{2}{7}}$，解得a₄=$\frac{1}{5}$.当n=3时，可求得a₅=$\frac{2}{13}$，则这列数为$\frac{2}{1}$，$\frac{2}{4}$，$\frac{2}{7}$，$\frac{2}{10}$，$\frac{2}{13}$，……，可以看出，分子为2，分母为3n-2，
∴第n个数为$\frac{2}{3n-2}$，
∴a₂₀₂₃=$\frac{2}{3×2023-2}$=$\frac{2}{6067}$.

5. (七中育才)我们可以用符号$f(a)$表示代数式.当a是正整数时,我们规定:如果a为偶数,$f(a)= 0.5a$;如果a为奇数,$f(a)= 3a+1$.例如：$f(20)= 10,f(5)= 16$.设$a_{1}= 2,a_{2}= f(a_{1}),a_{3}= f(a_{2}),... $,依此规律进行下去,得到一列数:$a_{1},a_{2},a_{3},a_{4},...,a_{n}$(n为正整数),则$a_{4}= $____;$5a_{1}-a_{2}+a_{3}-a_{4}+a_{5}-a_{6}+... +a_{2019}-a_{2020}+a_{2021}= $____.

答案： 2 12 【解析】由题意可得，a₁=2，a₂=f(a₁)=1，a₃=f(a₂)=4，a₄=2，a₅=1，……由此可得，这列数依次以2，1，4循环出现.
∵2021÷3=673……2，2021÷6=336……5，
∴5a₁-a₂+a₃-a₄+a₅-a₆+…+a₂₀₁₉-a₂₀₂₀+a₂₀₂₁=4a₁+(a₁-a₂+a₃)-(a₄-a₅+a₆)+(a₇-a₈+a₉)-…+(a₂₀₁₇-a₂₀₁₈+a₂₀₁₉)-(a₂₀₂₀-a₂₀₂₁)=4×2+[(a₁-a₂+a₃)-(a₄-a₅+a₆)]+…+[(a₂₀₁₇-a₂₀₁₈+a₂₀₁₉)-(a₂₀₂₀-a₂₀₂₁)]=8+0×336+[(2-1+4)-(2-1)]=8+0+(5-1)=8+0+4=12.

6. (青羊区期末)已知$1+3= 4= 2^{2},1+3+5= 9= 3^{2},1+3+5+7= 16= 4^{2},1+3+5+7+9= 25= 5^{2},... $,根据前面各式的规律,以下等式(n为正整数):①$1+3+5+7+9+... +(2n-1)= n^{2}$;②$1+3+5+7+9+... +(2n+3)= (n+3)^{2}$;③$1+3+5+7+9+... +2013= 1007^{2}$;④$101+103+105+107+... +2013= 1007^{2}-50^{2}$.其中正确的有____个.

答案： 3

7. (龙泉驿区期中)观察下列数表规律,第n列第二排的数为____.(用含n的代数式表示)

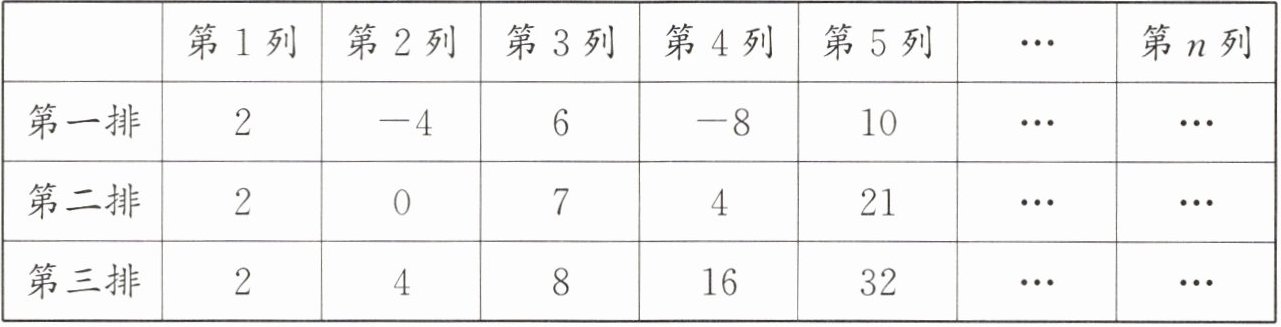
答案： $\frac{(-1)^{n+1}2n+2^n}{2}$ 【解析】
∵第一排第n列的数为(-1)ⁿ⁺¹2n，第三排第n列的数为2ⁿ，
∴第n列第二排的数为$\frac{(-1)^{n+1}2n+2^n}{2}$.

8. (青羊区期末)将连续的正整数按以下规律排放,则位于第5行、第5列的数是____,第n行、第n列的数是____.

答案： 41 2n(n-1)+1 【解析】观察表格可知，第1行、第1列的数是1=2×0×1+1，第2行、第2列的数是5=2×1×2+1，第3行、第3列的数是13=2×2×3+1，第4行、第4列的数是25=2×3×4+1，……，所以第n行、第n列的数是2n(n-1)+1.当n=5时，2n(n-1)+1=2×5×4+1=41，即第5行、第5列的数是41.