《2025年名校题库七年级数学上册》

6.(七中育才)阅读下列材料：$|a|= \left\{\begin{array}{l} a(a＞0),\\ 0(a= 0),\\ -a(a＜0),\end{array} \right. 当a＞0$时,$\frac {|a|}{a}= \frac {a}{a}= 1$；当$a＜0$时,$\frac {|a|}{a}= \frac {-a}{a}= -1$。运用以上结论解决下面问题：
(1)已知$x$,$y$是有理数,当$xy＞0$时,$\frac {|x|}{x}+\frac {|y|}{y}= $____；
(2)已知$x$,$y$,$z$是有理数,当$xyz＜0$时,求$\frac {|x|}{x}+\frac {|y|}{y}+\frac {|z|}{z}$的值；
(3)已知$x$,$y$,$z$是有理数,$x+y+z= 0$,且$xyz＜0$,求$\frac {|x|}{y+z}+\frac {|y|}{x+z}-\frac {|z|}{x+y}$的值。

答案：
(1) 解：因为 $xy ＞ 0$，所以 $x$，$y$ 同号。
当 $x ＞ 0$，$y ＞ 0$ 时，$\frac{|x|}{x} + \frac{|y|}{y} = 1 + 1 = 2$；
当 $x ＜ 0$，$y ＜ 0$ 时，$\frac{|x|}{x} + \frac{|y|}{y} = -1 + (-1) = -2$。
故答案为：$\pm 2$
(2) 解：因为 $xyz ＜ 0$，所以 $x$，$y$，$z$ 中有 1 个负数或 3 个负数。
当有 1 个负数时，不妨设 $x ＜ 0$，$y ＞ 0$，$z ＞ 0$，则$\frac{|x|}{x} + \frac{|y|}{y} + \frac{|z|}{z} = -1 + 1 + 1 = 1$；
当有 3 个负数时，$x ＜ 0$，$y ＜ 0$，$z ＜ 0$，则$\frac{|x|}{x} + \frac{|y|}{y} + \frac{|z|}{z} = -1 + (-1) + (-1) = -3$。
故答案为：$1$ 或 $-3$
(3) 解：因为 $x + y + z = 0$，所以 $y + z = -x$，$x + z = -y$，$x + y = -z$。
又因为 $xyz ＜ 0$，所以 $x$，$y$，$z$ 中有 1 个负数，2 个正数。
不妨设 $x ＜ 0$，$y ＞ 0$，$z ＞ 0$，则 $y + z = -x ＞ 0$，$x + z = -y ＜ 0$，$x + y = -z ＜ 0$。
所以$\frac{|x|}{y + z} + \frac{|y|}{x + z} - \frac{|z|}{x + y} = \frac{-x}{-x} + \frac{y}{-y} - \frac{z}{-z} = 1 - 1 + 1 = 1$。
故答案为：$1$

1. (金牛区期末)已知有理数$a,b,c$在数轴上对应点的位置如图所示,则$|c-b|-|a-b|+|a-c|$化简后的结果是______.

答案： 2c-2a

2. (锦江区期末)数$a,b,c$在数轴上对应点的位置如图所示,化简:$|a+c|-2|c-b|+|a-b|= $______.

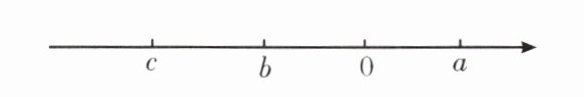
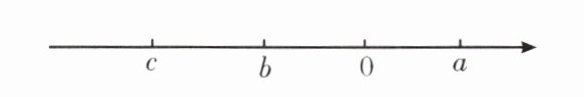
答案： -3b+c

3. (武侯区期末)已知$a,b,c$在数轴上对应点的位置如图所示,化简:$|a+b|+|c-b|-|a-c|= $______.

答案： -2b

4. (天府新区期末)已知有理数$a,b,c$在数轴上对应点的位置如图所示,化简:$2|a-b|+3|c-b|-|3c+a|= $______.

答案： -3a-b

5. (龙泉驿区期中)已知有理数$a,b,c$在数轴上的位置如图所示,且满足$|a|＜|b|＜|c|$,则$|2a+c-b|-|a-c+b|+\frac {ab}{|ab|}-\frac {|ac|}{ac}= $______.

答案： 3a-2

6. (成外)已知$a＜-1,-1≤c≤0,a\lt b\lt c$,则$|a+b+c|-|b-c|-|a-c-1|$的最小值为______,最大值为______.

答案： -1 2