《2025年名校题库七年级数学上册》

1.(金牛区期末)如图,$∠AOB= 20^{\circ },∠BOC= 80^{\circ }$,OE 是$∠AOC$的平分线,则$∠COE$的度数为 ( )

A.$50^{\circ }$
B.$40^{\circ }$
C.$30^{\circ }$
D.$20^{\circ }$

答案： A

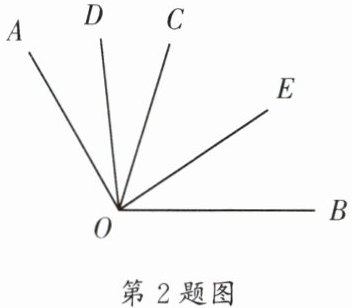
2.(成华区期末)如图,在$∠AOB$内部作射线 OC,再分别作$∠AOC和∠BOC$的平分线 OD,OE.若$∠AOB= 120^{\circ }$,则$∠DOE= $____.

答案： 60°

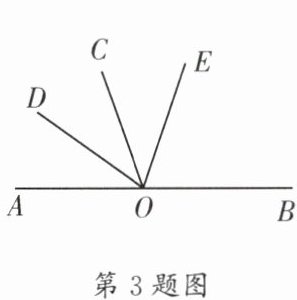
3.(锦江区期末)如图,O 为直线 AB 上的一点,射线 OD 平分$∠AOC$,射线 OE 平分$∠BOD$,且$∠BOC= 3∠AOD$,则$∠COE$的度数为____.

答案： 36°

4.(温江区期末)我们定义:若两个角差的绝对值等于$60^{\circ }$,则称这两个角互为“正角”,其中一个角是另一个角的“正角”.如:$∠1= 110^{\circ },∠2= 50^{\circ },|∠1-∠2|= 60^{\circ }$,则$∠1和∠2$互为“正角”.如图,已知$∠AOB= 120^{\circ }$,射线 OC 平分$∠AOB,∠EOF在∠AOB$的内部,若$∠EOF= 60^{\circ }$,则图中互为“正角”的角共有____对.

答案： 7

5.(石室联中)如图,OD 平分$∠AOB$,OE 平分$∠BOC,∠COD= 20^{\circ },∠AOB= 140^{\circ }$,求$∠DOE$的度数.

答案： 解:
∵OD平分∠AOB,∠AOB=140°,
∴∠AOD=$\frac{1}{2}$∠AOB=70°,
∴∠BOC=∠AOB−∠AOD−∠COD=50°.
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=25°,
∴∠DOE=∠COD+∠COE=45°.

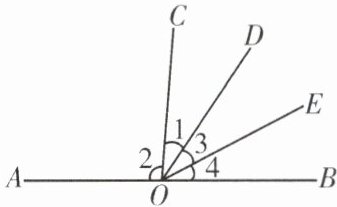
6.(武侯区期末)如图,已知 O 为直线 AB 上一点,过点 O 向直线 AB 上方引三条射线 OC,OD,OE,且 OE 平分$∠BOD,∠1= \frac {1}{3}∠2,∠COE= 58^{\circ }$,求$∠2$的度数.

答案： 解:
∵OE平分∠BOD,
∴∠3=∠4=$\frac{1}{2}$∠BOD.
∵∠BOD=180°−∠AOD,
∴∠3=$\frac{1}{2}$(180°−∠AOD)=90°−$\frac{1}{2}$(∠1+∠2).
∵∠1=$\frac{1}{3}$∠2,
∴∠3=90°−$\frac{1}{2}$(∠1+3∠1)=90°−2∠1,
∵∠1+∠3=∠COE=58°,
∴∠3=58°−∠1,
∴90°−2∠1=58°−∠1,
∴∠1=32°,
∴∠2=3∠1=96°.