《2025年名校题库七年级数学上册》

4.(武侯区期末)现用棱长为2厘米的小立方体按如图所示规律搭建几何体,图中自上而下分别叫第一层、第二层、第三层、…,其中第一层摆放1个小立方体,第二层摆放3个小立方体,第三层摆放6个小立方体,…,那么搭建第1个几何体需要1个小立方体,搭建第2个几何体需要4个小立方体,搭建第3个几何体需要10个小立方体,…,按此规律继续摆放.

(1)搭建第4个几何体需要小立方体的个数为______.
(2)为了美观,需将几何体的所有露出部分(不包含底面)都喷涂油漆,且喷涂1平方厘米需用油漆0.3克.
①喷涂第4个几何体需要油漆多少克?
②如果要求从第1个几何体开始,依次对第1个几何体、第2个几何体、第3个几何体、…、第n个几何体(其中n为正整数)进行喷涂油漆,那么当喷涂完第20个几何体时,共用掉油漆多少克?
[参考公式:①$1×2+2×3+3×4+... +n(n+1)= \frac {n(n+1)(n+2)}{3}$;②$1^{2}+2^{2}+3^{2}+... +n^{2}= \frac {n(n+1)(2n+1)}{6}$,其中n为正整数]

答案：
(1)20个
(2)解:①$5×(1+2+3+4)×2^{2}×0.3=60$(克).
②$5×[1+(1+2)+(1+2+3)+(1+2+3+4)+... +(1+2+3+... +20)]×2^{2}×0.3$
$=5×[\frac {1}{2}×\frac {20×(20+1)×(20+2)}{3}]×2^{2}×0.3$
$=5×1540×4×0.3$
$=9240$(克).

5.(实外)如图所示的几何体是由若干个棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.

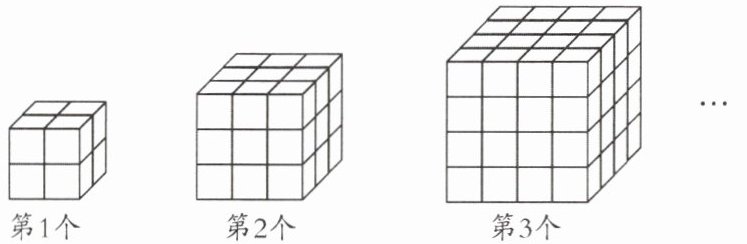
(1)第1个几何体中只有2个面涂色的小立方体共有______个,第3个几何体中只有2个面涂色的小立方体共有______个;
(2)求第100个几何体中只有2个面涂色的小立方体的个数;
(3)求前100个几何体中只有2个面涂色的小立方体的个数的和.

答案：
(1)4 20
(2)解:$8×100-4=796$(个).
(3)解:$(8×1-4)+(8×2-4)+... +(8×100-4)$
$=8×(1+2+3+... +100)-4×100$
$=40000$(个).