《2025年假期伴你行暑假合肥工业大学出版社七年级数学沪科版》

13. (西藏中考)解不等式组 $ \left\{ \begin{array} { l } { 3 x - 2 ＞ 1, } \\ { \frac { 2 x - 1 } { 3 } ＞ x - 2, } \end{array} \right. $ 并把解集在数轴上表示出来.

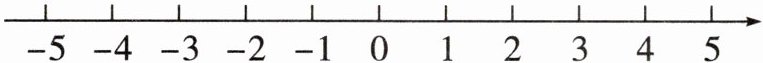
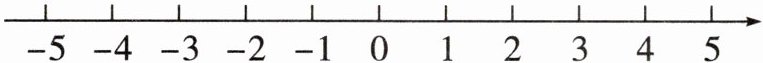
答案： 解：$\begin{cases}3x - 2 ＞ 1,①\\frac{2x - 1}{3} ＞ x - 2,②\end{cases}$
解不等式①，得$3x ＞ 1 + 2$，$3x ＞ 3$，$x ＞ 1$。
解不等式②，得$2x - 1 ＞ 3(x - 2)$，$2x - 1 ＞ 3x - 6$，$2x - 3x ＞ -6 + 1$，$-x ＞ -5$，$x ＜ 5$。
所以原不等式组的解集为$1 ＜ x ＜ 5$。
在数轴上表示解集：（在给定数轴上，1处画空心圆圈向右画线，5处画空心圆圈向左画线，两线相交部分为解集）

14. (荆门中考)已知关于 $ x $ 的不等式 $ 3 x - m + 1 ＞ 0 $ 的最小整数解为 $ 2 $,则实数 $ m $ 的取值范围是 (A)
A.$ 4 \leq m ＜ 7 $
B.$ 4 ＜ m ＜ 7 $
C.$ 4 \leq m \leq 7 $
D.$ 4 ＜ m \leq 7 $

答案： 解：解不等式 $3x - m + 1 ＞ 0$，得 $x ＞ \frac{m - 1}{3}$。
因为不等式的最小整数解为 2，所以 $1 \leq \frac{m - 1}{3} ＜ 2$。
解 $1 \leq \frac{m - 1}{3}$，得 $m - 1 \geq 3$，即 $m \geq 4$；
解 $\frac{m - 1}{3} ＜ 2$，得 $m - 1 ＜ 6$，即 $m ＜ 7$。
综上，$4 \leq m ＜ 7$。
答案：A

15. (南充中考)若关于 $ x $ 的不等式组 $ \left\{ \begin{array} { l } { 2 x - 1 ＜ 5, } \\ { x ＜ m + 1 } \end{array} \right. $ 的解集为 $ x ＜ 3 $,则 $ m $ 的取值范围是 (B)
A.$ m ＞ 2 $
B.$ m \geq 2 $
C.$ m ＜ 2 $
D.$ m \leq 2 $

答案： 解：解不等式 $2x - 1 ＜ 5$，得 $x ＜ 3$。
因为不等式组的解集为 $x ＜ 3$，且另一个不等式为 $x ＜ m + 1$，所以 $m + 1 \geq 3$，解得 $m \geq 2$。
答案：B

16. (黑龙江中考)关于 $ x $ 的不等式组 $ \left\{ \begin{array} { l } { 4 - 2 x \geq 0, } \\ { \frac { 1 } { 2 } x - a ＞ 0 } \end{array} \right. $ 恰有 $ 3 $ 个整数解,则 $ a $ 的取值范围是$-\frac{1}{2} \leq a ＜ 0$.

答案： 解：解不等式组$\left\{ \begin{array}{l} 4 - 2x \geq 0 \\ \frac{1}{2}x - a ＞ 0 \end{array} \right.$
解第一个不等式：$4 - 2x \geq 0$
$-2x \geq -4$
$x \leq 2$
解第二个不等式：$\frac{1}{2}x - a ＞ 0$
$\frac{1}{2}x ＞ a$
$x ＞ 2a$
所以不等式组的解集为$2a ＜ x \leq 2$
因为不等式组恰有3个整数解，即$0$，$1$，$2$
所以$-1 \leq 2a ＜ 0$
解得$-\frac{1}{2} \leq a ＜ 0$
$-\frac{1}{2} \leq a ＜ 0$

17. (宜宾中考)若关于 $ x $ 的不等式组 $ \left\{ \begin{array} { l } { 2 x + 1 ＞ x + a, } \\ { \frac { x } { 2 } + 1 \geq \frac { 5 } { 2 } x - 9 } \end{array} \right. $ 所有整数解的和为 $ 14 $,则整数 $ a $ 的值为______2或-1.

答案： 解：解不等式$2x + 1 ＞ x + a$，得$x ＞ a - 1$。
解不等式$\frac{x}{2} + 1 \geq \frac{5}{2}x - 9$，得$x \leq 5$。
所以不等式组的解集为$a - 1 ＜ x \leq 5$。
因为不等式组所有整数解的和为$14$，整数解可能为$2,3,4,5$或$3,4,5,2$（顺序不影响和），其和为$2 + 3 + 4 + 5 = 14$；或整数解为$5,4,3,2$，也可能为$5,4,3,2$之外的情况，经分析另一种可能是整数解为$5,4,3,2$不成立时，考虑整数解为$5,4,3,2$的前几个数，若整数解为$5,4,3,2$，则$a - 1$的范围是$1 \leq a - 1 ＜ 2$，解得$2 \leq a ＜ 3$，此时$a$为整数$2$；若整数解为$4,5,3,2$不成立，另一种情况整数解为$5,4,3,2$不满足时，考虑整数解为$5,4,3,2$的前部分，若整数解为$5,4,3,2$不成立，当整数解为$5,4,3,2$的前几个数，若整数解为$5,4,3,2$不成立，当$a - 1$在$-2 \leq a - 1 ＜ -1$时，整数解为$-1,0,1,2,3,4,5$，和为$-1 + 0 + 1 + 2 + 3 + 4 + 5 = 14$，此时$a - 1$的范围是$-2 \leq a - 1 ＜ -1$，解得$-1 \leq a ＜ 0$，$a$为整数$-1$。
综上，整数$a$的值为$2$或$-1$。
答案：$2$或$-1$

18. (宜宾中考)某单位为响应政府号召,需要购买分类垃圾桶 $ 6 $ 个,市场上有 $ A $ 型和 $ B $ 型两种分类垃圾桶,$ A $ 型分类垃圾桶 $ 500 $ 元/个,$ B $ 型分类垃圾桶 $ 550 $ 元/个,总费用不超过 $ 3100 $ 元,则不同的购买方案有 (B)
A.$ 2 $ 种
B.$ 3 $ 种
C.$ 4 $ 种
D.$ 5 $ 种

答案： 解：设购买A型分类垃圾桶$x$个，则购买B型分类垃圾桶$(6 - x)$个。
根据题意，得$500x + 550(6 - x) \leq 3100$。
解得$x \geq 4$。
因为$x$为非负整数，且$6 - x \geq 0$，即$x \leq 6$，所以$x$可取4，5，6。
当$x = 4$时，$6 - x = 2$；
当$x = 5$时，$6 - x = 1$；
当$x = 6$时，$6 - x = 0$。
共有3种购买方案。
答案：B

19. (攀枝花中考)某学校准备购进单价分别为 $ 5 $ 元和 $ 7 $ 元的 $ A $,$ B $ 两种笔记本共 $ 50 $ 本作为奖品发放给学生,要求 $ A $ 种笔记本的数量不多于 $ B $ 种笔记本数量的 $ 3 $ 倍,不少于 $ B $ 种笔记本数量的 $ 2 $ 倍,则不同的购买方案种数为 (D)
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $

答案： 解：设购进A种笔记本$x$本，则购进B种笔记本$(50-x)$本。
由题意得：
$\begin{cases}x \leq 3(50 - x) \\x \geq 2(50 - x)\end{cases}$
解第一个不等式：
$x \leq 150 - 3x$
$4x \leq 150$
$x \leq 37.5$
解第二个不等式：
$x \geq 100 - 2x$
$3x \geq 100$
$x \geq \frac{100}{3} \approx 33.33$
因为$x$为整数，所以$x$可取34，35，36，37。
即不同的购买方案有4种。
答案：D

20. (泸州中考)某商场购进 $ A $,$ B $ 两种商品,已知购进 $ 3 $ 件 $ A $ 商品比购进 $ 4 $ 件 $ B $ 商品费用多 $ 60 $ 元；购进 $ 5 $ 件 $ A $ 商品和 $ 2 $ 件 $ B $ 商品总费用为 $ 620 $ 元.
(1)求 $ A $,$ B $ 两种商品每件进价各为多少元；
(2)该商场计划购进 $ A $,$ B $ 两种商品共 $ 60 $ 件,且购进 $ B $ 商品的件数不少于 $ A $ 商品件数的 $ 2 $ 倍. 若 $ A $ 商品按每件 $ 150 $ 元销售,$ B $ 商品按每件 $ 80 $ 元销售,为满足销售完 $ A $,$ B $ 两种商品后获得的总利润不低于 $ 1770 $ 元,则购进 $ A $ 商品的件数最多为多少?

答案：
(1)设A商品的进价是x元/件，B商品的进价是y元/件。根据题意，得
$\begin{cases}3x - 4y = 60\\5x + 2y = 620\end{cases}$
解得$\begin{cases}x = 100\\y = 60\end{cases}$
答：A商品的进价是100元/件，B商品的进价是60元/件。
(2)设购进m件A商品，则购进(60 - m)件B商品。根据题意，得
$\begin{cases}60 - m \geq 2m\\(150 - 100)m + (80 - 60)(60 - m) \geq 1770\end{cases}$
解得$19 \leq m \leq 20$
所以m的最大值为20。
答：购进A商品的件数最多为20件。