《2025年假期伴你行暑假合肥工业大学出版社七年级数学沪科版》

26. 已知$a$的平方等于4,$b$的算术平方根等于4,$c$的立方等于8,$d$的立方根等于8。
(1)求$a,b,c,d$的值；
(2)求$\sqrt {d÷(bc)}+a$的值。

答案：
(1)解：因为$a^2 = 4$，所以$a = \pm 2$；
因为$\sqrt{b} = 4$，所以$b = 16$；
因为$c^3 = 8$，所以$c = 2$；
因为$\sqrt[3]{d} = 8$，所以$d = 512$。
(2)解：当$a = 2$时，$\sqrt{d÷(bc)} + a = \sqrt{512÷(16×2)} + 2 = \sqrt{512÷32} + 2 = \sqrt{16} + 2 = 4 + 2 = 6$；
当$a = -2$时，$\sqrt{d÷(bc)} + a = \sqrt{512÷(16×2)} - 2 = \sqrt{16} - 2 = 4 - 2 = 2$。
故$\sqrt{d÷(bc)} + a$的值为$6$或$2$。

27. (1)填空：①$\sqrt {1×3+1}=$2；
②$\sqrt {2×4+1}=$3；
③$\sqrt {3×5+1}=$4；
④$\sqrt {4×6+1}=$5。
(2)根据上面的算式,你发现了什么规律,请用公式表示出来。
规律：对于正整数n，$\sqrt{n(n+2)+1}=n+1$

答案：
(1)①2 ②3 ③4 ④5
(2)规律：对于正整数n，$\sqrt{n(n+2)+1}=n+1$

28. 在实数范围内定义一种新运算“$\triangle $”,其规则为$a\triangle b= \sqrt {a}-\sqrt {b}$,根据这个规则：
(1)求$16\triangle 9$的值；
(2)求$(x+2)^{2}\triangle 25= 0中x$的值。

答案：
(1) $16\triangle 9 = \sqrt{16} - \sqrt{9} = 4 - 3 = 1$
(2) 由题意，得 $\sqrt{(x+2)^2} - \sqrt{25} = 0$
$\sqrt{(x+2)^2} = 5$
$|x+2| = 5$
则 $x+2 = 5$ 或 $x+2 = -5$
解得 $x = 3$ 或 $x = -7$

29. 现有两块同样大小的长方形木板①,②,甲木工采用如图1所示的方式,在长方形木板①上截出三个面积分别为$4dm^{2},8dm^{2}和18dm^{2}的正方形木板A,B,C$。

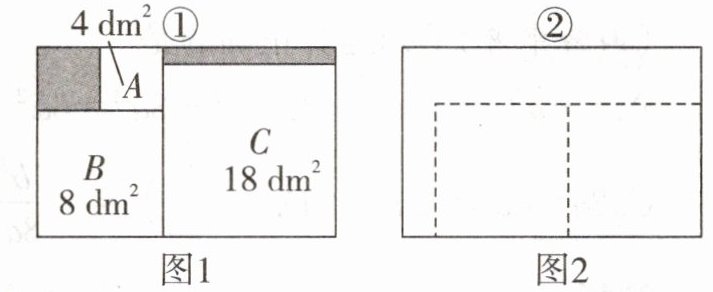
(1)木板①中截出的正方形木板$C$的边长为$3\sqrt{2}$$dm$；
(2)木板①中剩余部分(阴影部分)的面积是$10\sqrt{2} - 10$$dm^{2}$；
(3)乙木工想采用如图2所示的方式,在长方形木板②上截出两个面积均为$16dm^{2}$的正方形木板,请你判断能否截出,并说明理由。
不能。理由如下：
由图1知，长方形木板的长为 $\sqrt{18} + \sqrt{8} = 3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\,dm$。
两个面积为 $16\,dm^2$ 的正方形边长均为 $\sqrt{16} = 4\,dm$，总长度为 $4 × 2 = 8\,dm$。
因为 $5\sqrt{2} \approx 7.07 ＜ 8$，所以不能截出。

答案：
(1) $3\sqrt{2}$
(2) $10\sqrt{2} - 10$
(3) 不能。理由如下：
由图1知，长方形木板的长为 $\sqrt{18} + \sqrt{8} = 3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\,dm$。
两个面积为 $16\,dm^2$ 的正方形边长均为 $\sqrt{16} = 4\,dm$，总长度为 $4 × 2 = 8\,dm$。
因为 $5\sqrt{2} \approx 7.07 ＜ 8$，所以不能截出。