第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
11. 定义一种运算:$a*b= \left\{\begin{array}{l} a(a≥b),\\ b(a<b),\end{array} \right. 则不等式(2x+1)*(2-x)>3$的解集是 (
A.$x>1或x<\frac {1}{3}$
B.$-1<x<\frac {1}{3}$
C.$x>1或x<-1$
D.$x>\frac {1}{3}或x<-1$
C
)A.$x>1或x<\frac {1}{3}$
B.$-1<x<\frac {1}{3}$
C.$x>1或x<-1$
D.$x>\frac {1}{3}或x<-1$
答案:
解:由定义知,$a*b$取$a$、$b$中的较大值。
情况1:当$2x + 1 \geq 2 - x$,即$x \geq \frac{1}{3}$时
此时$(2x + 1)*(2 - x) = 2x + 1$,不等式为:
$2x + 1 > 3$
解得$x > 1$
结合前提$x \geq \frac{1}{3}$,得$x > 1$
情况2:当$2x + 1 < 2 - x$,即$x < \frac{1}{3}$时
此时$(2x + 1)*(2 - x) = 2 - x$,不等式为:
$2 - x > 3$
解得$x < -1$
结合前提$x < \frac{1}{3}$,得$x < -1$
综上,解集为$x > 1$或$x < -1$。
答案:C
情况1:当$2x + 1 \geq 2 - x$,即$x \geq \frac{1}{3}$时
此时$(2x + 1)*(2 - x) = 2x + 1$,不等式为:
$2x + 1 > 3$
解得$x > 1$
结合前提$x \geq \frac{1}{3}$,得$x > 1$
情况2:当$2x + 1 < 2 - x$,即$x < \frac{1}{3}$时
此时$(2x + 1)*(2 - x) = 2 - x$,不等式为:
$2 - x > 3$
解得$x < -1$
结合前提$x < \frac{1}{3}$,得$x < -1$
综上,解集为$x > 1$或$x < -1$。
答案:C
12. 某班级奖励“德、智、体、美、劳”五育表现优异的学生,计划用不超过100元购买A,B两种笔记本作为奖品,A种笔记本每本8元,B种笔记本每本10元,每种笔记本至少买4本,则购买方案有 (
A.7种
B.8种
C.9种
D.10种
C
)A.7种
B.8种
C.9种
D.10种
答案:
解:设购买A种笔记本x本,B种笔记本y本。
根据题意,得:
$\begin{cases}8x + 10y \leq 100 \\x \geq 4 \\y \geq 4 \\x,y为正整数\end{cases}$
由$x \geq 4$,$y \geq 4$,得$8×4 + 10×4 = 72 \leq 8x + 10y \leq 100$,即$0 \leq 8(x - 4) + 10(y - 4) \leq 28$。
设$a = x - 4$,$b = y - 4$,则$a,b \geq 0$且为整数,$8a + 10b \leq 28$,化简得$4a + 5b \leq 14$。
当$b = 0$时,$4a \leq 14$,$a \leq 3.5$,$a = 0,1,2,3$,共4种;
当$b = 1$时,$4a \leq 9$,$a \leq 2.25$,$a = 0,1,2$,共3种;
当$b = 2$时,$4a \leq 4$,$a \leq 1$,$a = 0,1$,共2种;
当$b \geq 3$时,$5b \geq 15 > 14$,无解。
总方案数:$4 + 3 + 2 = 9$种。
答案:C
根据题意,得:
$\begin{cases}8x + 10y \leq 100 \\x \geq 4 \\y \geq 4 \\x,y为正整数\end{cases}$
由$x \geq 4$,$y \geq 4$,得$8×4 + 10×4 = 72 \leq 8x + 10y \leq 100$,即$0 \leq 8(x - 4) + 10(y - 4) \leq 28$。
设$a = x - 4$,$b = y - 4$,则$a,b \geq 0$且为整数,$8a + 10b \leq 28$,化简得$4a + 5b \leq 14$。
当$b = 0$时,$4a \leq 14$,$a \leq 3.5$,$a = 0,1,2,3$,共4种;
当$b = 1$时,$4a \leq 9$,$a \leq 2.25$,$a = 0,1,2$,共3种;
当$b = 2$时,$4a \leq 4$,$a \leq 1$,$a = 0,1$,共2种;
当$b \geq 3$时,$5b \geq 15 > 14$,无解。
总方案数:$4 + 3 + 2 = 9$种。
答案:C
13. 不等式$x+2≥0$的解集是
$x \geq -2$
.
答案:
解:$x+2 \geq 0$
$x \geq -2$
$x \geq -2$
14. 用“>”或“<”填空:若$a<b<0$,则$-\frac {a}{5}$
>
$-\frac {b}{5}$;$2a-1$<
$2b-1$.
答案:
解:因为$a < b < 0$,所以$-a > -b$,两边同时除以$5$,得$-\frac{a}{5} > -\frac{b}{5}$;
因为$a < b$,两边同时乘以$2$,得$2a < 2b$,两边同时减$1$,得$2a - 1 < 2b - 1$。
$>$;$<$
因为$a < b$,两边同时乘以$2$,得$2a < 2b$,两边同时减$1$,得$2a - 1 < 2b - 1$。
$>$;$<$
15. 不等式$7x+5<5x+1$的解集为
$x<-2$
.
答案:
解:$7x + 5 < 5x + 1$
$7x - 5x < 1 - 5$
$2x < -4$
$x < -2$
$x < -2$
$7x - 5x < 1 - 5$
$2x < -4$
$x < -2$
$x < -2$
16. 不等式组$\left\{\begin{array}{l} x-2>0,\\ x-3<0\end{array} \right. $的解集是
2<x<3
.
答案:
解:解不等式$x - 2 > 0$,得$x > 2$;
解不等式$x - 3 < 0$,得$x < 3$;
所以不等式组的解集是$2 < x < 3$。
解不等式$x - 3 < 0$,得$x < 3$;
所以不等式组的解集是$2 < x < 3$。
17. 某商家花费855元购进某种水果90kg,销售中有5%的水果损耗,为确保不亏本,售价至少应定为
10
元/千克.
答案:
解:设售价应定为$x$元/千克。
水果损耗后剩余质量为:$90×(1 - 5\%) = 90×0.95 = 85.5$(kg)
要确保不亏本,则$85.5x \geq 855$
解得$x \geq 10$
答:售价至少应定为10元/千克。
水果损耗后剩余质量为:$90×(1 - 5\%) = 90×0.95 = 85.5$(kg)
要确保不亏本,则$85.5x \geq 855$
解得$x \geq 10$
答:售价至少应定为10元/千克。
18. 若关于x的一元一次不等式组$\left\{\begin{array}{l} \frac {x+3}{2}≤4,\\ 2x-a≥2\end{array} \right. $至少有2个整数解,则a的取值范围是____
$a \leq 6$
.
答案:
解:解不等式$\frac{x + 3}{2} \leq 4$,得$x + 3 \leq 8$,$x \leq 5$。
解不等式$2x - a \geq 2$,得$2x \geq a + 2$,$x \geq \frac{a + 2}{2}$。
所以不等式组的解集为$\frac{a + 2}{2} \leq x \leq 5$。
因为不等式组至少有2个整数解,所以整数解至少为4,5。
则$\frac{a + 2}{2} \leq 4$,解得$a + 2 \leq 8$,$a \leq 6$。
故$a$的取值范围是$a \leq 6$。
解不等式$2x - a \geq 2$,得$2x \geq a + 2$,$x \geq \frac{a + 2}{2}$。
所以不等式组的解集为$\frac{a + 2}{2} \leq x \leq 5$。
因为不等式组至少有2个整数解,所以整数解至少为4,5。
则$\frac{a + 2}{2} \leq 4$,解得$a + 2 \leq 8$,$a \leq 6$。
故$a$的取值范围是$a \leq 6$。
19. 关于x的不等式$m-\frac {x}{2}≤1-x$有正数解,m的值可以是____
0
(写出一个即可).
答案:
解:解不等式$m - \frac{x}{2} \leq 1 - x$,
移项得:$-\frac{x}{2} + x \leq 1 - m$,
合并同类项得:$\frac{x}{2} \leq 1 - m$,
两边同乘$2$得:$x \leq 2(1 - m)$。
因为不等式有正数解,所以$2(1 - m) > 0$,
解得$m < 2$,
则$m$的值可以是$0$。
0
移项得:$-\frac{x}{2} + x \leq 1 - m$,
合并同类项得:$\frac{x}{2} \leq 1 - m$,
两边同乘$2$得:$x \leq 2(1 - m)$。
因为不等式有正数解,所以$2(1 - m) > 0$,
解得$m < 2$,
则$m$的值可以是$0$。
0
20. (4分)解不等式$\frac {3x-2}{2}≤2$,并把它的解集表示在数轴上.
答案:
解:去分母,得 $ 3x - 2 \leq 4 $。移项,得 $ 3x \leq 4 + 2 $。合并同类项,得 $ 3x \leq 6 $。系数化为 1,得 $ x \leq 2 $。将不等式的解集表示在数轴上如图所示:
解:去分母,得 $ 3x - 2 \leq 4 $。移项,得 $ 3x \leq 4 + 2 $。合并同类项,得 $ 3x \leq 6 $。系数化为 1,得 $ x \leq 2 $。将不等式的解集表示在数轴上如图所示:

21. (8分)解不等式组$\left\{\begin{array}{l} 2x+1≤3,①\\ 3x-1≥x-7.②\end{array} \right. $
请结合题意填空,完成本题的解答.
(1)解不等式①,得____;
(2)解不等式②,得____;
(3)把不等式①和②的解集在数轴上表示出来;
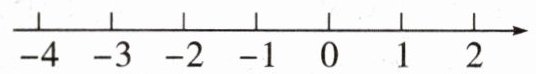
(4)原不等式组的解集为____.
请结合题意填空,完成本题的解答.
(1)解不等式①,得____;
(2)解不等式②,得____;
(3)把不等式①和②的解集在数轴上表示出来;
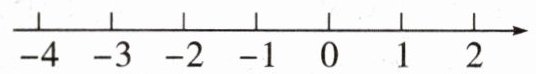
(4)原不等式组的解集为____.
答案:
解:(1)$ x \leq 1 $ (2)$ x \geq -3 $
(3)将不等式①和②的解集在数轴上表示出来,如图所示:

(4)$ -3 \leq x \leq 1 $
解:(1)$ x \leq 1 $ (2)$ x \geq -3 $
(3)将不等式①和②的解集在数轴上表示出来,如图所示:

(4)$ -3 \leq x \leq 1 $
22. (6分)x取哪些正整数值时,不等式$5x+2>3(x-1)与\frac {2x-1}{3}≤\frac {3x+1}{6}$都成立?
答案:
解:根据题意,解不等式组$\begin{cases}5x + 2 > 3(x - 1)① \\ \frac{2x - 1}{3} \leq \frac{3x + 1}{6}②\end{cases}$
解不等式①:
$5x + 2 > 3x - 3$
$5x - 3x > -3 - 2$
$2x > -5$
$x > -\frac{5}{2}$
解不等式②:
$2(2x - 1) \leq 3x + 1$
$4x - 2 \leq 3x + 1$
$4x - 3x \leq 1 + 2$
$x \leq 3$
所以不等式组的解集为$-\frac{5}{2} < x \leq 3$,满足条件的正整数有1,2,3。
解不等式①:
$5x + 2 > 3x - 3$
$5x - 3x > -3 - 2$
$2x > -5$
$x > -\frac{5}{2}$
解不等式②:
$2(2x - 1) \leq 3x + 1$
$4x - 2 \leq 3x + 1$
$4x - 3x \leq 1 + 2$
$x \leq 3$
所以不等式组的解集为$-\frac{5}{2} < x \leq 3$,满足条件的正整数有1,2,3。
查看更多完整答案,请扫码查看


