第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. $-\frac{1}{2025}$的相反数(
A.2025
B.$\frac{1}{2025}$
C.-2025
D.$-\frac{1}{2025}$
B
)A.2025
B.$\frac{1}{2025}$
C.-2025
D.$-\frac{1}{2025}$
答案:
解:根据相反数的定义,只有符号不同的两个数互为相反数。
$-\frac{1}{2025}$的相反数是$\frac{1}{2025}$。
答案:B
$-\frac{1}{2025}$的相反数是$\frac{1}{2025}$。
答案:B
2. $-\frac{1}{7}$的绝对值是(
A.-7
B.7
C.$-\frac{1}{7}$
D.$\frac{1}{7}$
D
)A.-7
B.7
C.$-\frac{1}{7}$
D.$\frac{1}{7}$
答案:
解:因为负数的绝对值是它的相反数,所以$-\frac{1}{7}$的绝对值是$\frac{1}{7}$。
答案:D
答案:D
3. -2的相反数的倒数是(
A.2
B.$\frac{1}{2}$
C.$-\frac{1}{2}$
D.-2
B
)A.2
B.$\frac{1}{2}$
C.$-\frac{1}{2}$
D.-2
答案:
-2的相反数是2,2的倒数是$\frac{1}{2}$,所以-2的相反数的倒数是$\frac{1}{2}$。
答案:B
答案:B
4. 下列四个数中,是正整数的是(
A.-1
B.0
C.$\frac{1}{2}$
D.1
D
)A.-1
B.0
C.$\frac{1}{2}$
D.1
答案:
解:正整数是指大于0的整数。
A.-1是负整数,不符合;
B.0既不是正数也不是负数,不符合;
C.$\frac{1}{2}$是分数,不符合;
D.1是正整数,符合。
答案:D
A.-1是负整数,不符合;
B.0既不是正数也不是负数,不符合;
C.$\frac{1}{2}$是分数,不符合;
D.1是正整数,符合。
答案:D
5. 若盈余2万元记作+2万元,则-2万元表示(
A.盈余2万元
B.亏损2万元
C.亏损-2万元
D.不盈余也不亏损
B
)A.盈余2万元
B.亏损2万元
C.亏损-2万元
D.不盈余也不亏损
答案:
解:
∵盈余2万元记作+2万元,
∴-2万元表示亏损2万元。
答案:B
∵盈余2万元记作+2万元,
∴-2万元表示亏损2万元。
答案:B
6. 2024年5月10日,记者从中国科学院国家天文台获悉,“中国天眼”FAST近期发现了6个距离地球约50亿光年的中性氢星系,这是人类迄今直接探测到的最远的一批中性氢星系.50亿光年用科学记数法表示为(
A.$50×10^{8}$光年
B.$5×10^{8}$光年
C.$5×10^{9}$光年
D.$5×10^{10}$光年
C
)A.$50×10^{8}$光年
B.$5×10^{8}$光年
C.$5×10^{9}$光年
D.$5×10^{10}$光年
答案:
解:50亿光年 = 5000000000光年 = $5×10^{9}$光年。
答案:C
答案:C
7. 在算式$3-|-5□2|$中的“□”,填入哪个运算符号能使得算式的值最大(
A.+
B.-
C.×
D.÷
D
)A.+
B.-
C.×
D.÷
答案:
解:分别将各选项代入运算符号“□”计算:
- 选项A(+):$3 - |-5 + 2| = 3 - |-3| = 3 - 3 = 0$
- 选项B(-):$3 - |-5 - 2| = 3 - |-7| = 3 - 7 = -4$
- 选项C(×):$3 - |-5×2| = 3 - |-10| = 3 - 10 = -7$
- 选项D(÷):$3 - |-5÷2| = 3 - |-2.5| = 3 - 2.5 = 0.5$
比较结果:$0.5 > 0 > -4 > -7$,故填入“÷”时算式的值最大。
答案:D
- 选项A(+):$3 - |-5 + 2| = 3 - |-3| = 3 - 3 = 0$
- 选项B(-):$3 - |-5 - 2| = 3 - |-7| = 3 - 7 = -4$
- 选项C(×):$3 - |-5×2| = 3 - |-10| = 3 - 10 = -7$
- 选项D(÷):$3 - |-5÷2| = 3 - |-2.5| = 3 - 2.5 = 0.5$
比较结果:$0.5 > 0 > -4 > -7$,故填入“÷”时算式的值最大。
答案:D
8. 小亮用天平称得一个罐头的质量为2.026kg,用四舍五入法将2.026精确到0.01的近似数为(
A.2
B.2.0
C.2.02
D.2.03
D
)A.2
B.2.0
C.2.02
D.2.03
答案:
2.026精确到0.01,即保留两位小数,看小数点后第三位数字是6,6>5,向前进1,所以2.026≈2.03。
答案:D
答案:D
9. 若$|x|= 5$,$|y|= 2$,且$x+y<0$,则$x-y$的值为(
A.7
B.3
C.-7或-3
D.-5
C
)A.7
B.3
C.-7或-3
D.-5
答案:
解:
∵|x|=5,|y|=2,
∴x=±5,y=±2。
∵x+y<0,
∴分两种情况:
①当x=-5,y=2时,x+y=-5+2=-3<0,符合题意,此时x-y=-5-2=-7;
②当x=-5,y=-2时,x+y=-5+(-2)=-7<0,符合题意,此时x-y=-5-(-2)=-3。
综上,x-y的值为-7或-3。
答案:C
∵|x|=5,|y|=2,
∴x=±5,y=±2。
∵x+y<0,
∴分两种情况:
①当x=-5,y=2时,x+y=-5+2=-3<0,符合题意,此时x-y=-5-2=-7;
②当x=-5,y=-2时,x+y=-5+(-2)=-7<0,符合题意,此时x-y=-5-(-2)=-3。
综上,x-y的值为-7或-3。
答案:C
10. 若m和n互为相反数,p和q互为倒数,a是最大的负整数,则$\frac{m+n}{2025}-2pq-3a$的值为(
A.1
B.2
C.3
D.5
A
)A.1
B.2
C.3
D.5
答案:
解:因为m和n互为相反数,所以m+n=0;
因为p和q互为倒数,所以pq=1;
因为a是最大的负整数,所以a=-1。
则原式=$\frac{0}{2025}-2×1-3×(-1)$
=0-2+3
=1
答案:A
因为p和q互为倒数,所以pq=1;
因为a是最大的负整数,所以a=-1。
则原式=$\frac{0}{2025}-2×1-3×(-1)$
=0-2+3
=1
答案:A
11. 北京与莫斯科的时差为5小时,例如,北京时间13:00,同一时刻的莫斯科时间是8:00.小丽和小红分别在北京和莫斯科,她们相约在各自当地时间9:00~17:00之间选择一个时刻开始通话,这个时刻可以是北京时间(
A.10:00
B.12:00
C.15:00
D.18:00
C
)A.10:00
B.12:00
C.15:00
D.18:00
答案:
解:设通话开始时的北京时间为$x$($9\leqslant x\leqslant17$)。
因为北京与莫斯科时差为5小时,且北京在东,莫斯科在西,所以莫斯科时间为$x - 5$。
小红在莫斯科,需满足当地时间$9\leqslant x - 5\leqslant17$,
即$9 + 5\leqslant x\leqslant17 + 5$,$14\leqslant x\leqslant22$。
又因小丽在北京,$9\leqslant x\leqslant17$,所以$x$需同时满足$14\leqslant x\leqslant17$。
选项中在此范围内的是15:00。
答案:C
因为北京与莫斯科时差为5小时,且北京在东,莫斯科在西,所以莫斯科时间为$x - 5$。
小红在莫斯科,需满足当地时间$9\leqslant x - 5\leqslant17$,
即$9 + 5\leqslant x\leqslant17 + 5$,$14\leqslant x\leqslant22$。
又因小丽在北京,$9\leqslant x\leqslant17$,所以$x$需同时满足$14\leqslant x\leqslant17$。
选项中在此范围内的是15:00。
答案:C
12. 有理数a,b在数轴上对应点所在的位置如图所示,则下列结论正确的是(
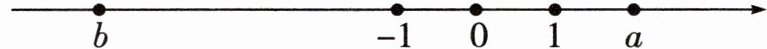
A.$|a|>|b|$
B.$ab>0$
C.$a+b>0$
D.$a-b>0$
D
)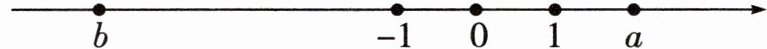
A.$|a|>|b|$
B.$ab>0$
C.$a+b>0$
D.$a-b>0$
答案:
由数轴可知:$b < -1$,$1 < a$。
A. $|a| < |b|$,故A错误;
B. $a > 0$,$b < 0$,$ab < 0$,故B错误;
C. $|a| < |b|$,且$b$为负数,$a + b < 0$,故C错误;
D. $a > 0$,$b < 0$,$-b > 0$,$a - b = a + (-b) > 0$,故D正确。
答案:D
A. $|a| < |b|$,故A错误;
B. $a > 0$,$b < 0$,$ab < 0$,故B错误;
C. $|a| < |b|$,且$b$为负数,$a + b < 0$,故C错误;
D. $a > 0$,$b < 0$,$-b > 0$,$a - b = a + (-b) > 0$,故D正确。
答案:D
13. 计算$\frac{2^{2}-1}{3}+\frac{3^{2}-2^{2}}{5}+\frac{4^{2}-3^{2}}{7}+...+\frac{2024^{2}-2023^{2}}{4047}= $
A.2022
B.2023
C.2024
D.2025
B
A.2022
B.2023
C.2024
D.2025
答案:
解:观察原式,第$n$项的分子为$(n+1)^2 - n^2$,分母为$2n + 1$($n$从1到2023)。
$\begin{aligned}\frac{(n+1)^2 - n^2}{2n + 1}&=\frac{n^2 + 2n + 1 - n^2}{2n + 1}\\&=\frac{2n + 1}{2n + 1}\\&=1\end{aligned}$
原式共有$2023$项,每项都为$1$,则总和为$2023×1 = 2023$。
答案:B
$\begin{aligned}\frac{(n+1)^2 - n^2}{2n + 1}&=\frac{n^2 + 2n + 1 - n^2}{2n + 1}\\&=\frac{2n + 1}{2n + 1}\\&=1\end{aligned}$
原式共有$2023$项,每项都为$1$,则总和为$2023×1 = 2023$。
答案:B
查看更多完整答案,请扫码查看


