《2025年假期伴你行暑假合肥工业大学出版社七年级数学沪科版》

8. 若$a^{2}-ab= 0(b≠0)$,则$\frac {a}{a+b}= $ (C)
A.0
B.$\frac {1}{2}$
C.0 或$\frac {1}{2}$
D.1 或 2

答案： 解：
∵ $a^2 - ab = 0$，
∴ $a(a - b) = 0$，
∴ $a = 0$ 或 $a = b$。
情况1：当 $a = 0$ 时，
$\frac{a}{a + b} = \frac{0}{0 + b} = 0$（$b \neq 0$）。
情况2：当 $a = b$ 时，
$\frac{a}{a + b} = \frac{a}{a + a} = \frac{a}{2a} = \frac{1}{2}$（$a = b \neq 0$）。
综上，$\frac{a}{a + b} = 0$ 或 $\frac{1}{2}$。
答案：C

9. 计算：$(\frac {a^{3}}{b^{2}})^{2}÷(\frac {a}{b^{3}})^{2}=$$a^{4}b^{2}$.

答案： 解：$(\frac{a^{3}}{b^{2}})^{2}÷(\frac{a}{b^{3}})^{2}$
$=\frac{a^{6}}{b^{4}}÷\frac{a^{2}}{b^{6}}$
$=\frac{a^{6}}{b^{4}}×\frac{b^{6}}{a^{2}}$
$=a^{4}b^{2}$
$a^{4}b^{2}$

10. 计算$\frac {x}{x+1}+\frac {2x}{x^{2}-1}$的结果为$\frac{x}{x - 1}$.

答案： 解：原式$=\frac{x}{x+1}+\frac{2x}{(x+1)(x-1)}$
$=\frac{x(x-1)}{(x+1)(x-1)}+\frac{2x}{(x+1)(x-1)}$
$=\frac{x(x-1)+2x}{(x+1)(x-1)}$
$=\frac{x^2 - x + 2x}{(x+1)(x-1)}$
$=\frac{x^2 + x}{(x+1)(x-1)}$
$=\frac{x(x + 1)}{(x+1)(x-1)}$
$=\frac{x}{x - 1}$
$\frac{x}{x - 1}$

11. 计算$(a-1-\frac {5}{a-5})\cdot \frac {2a-10}{6-a}=$$-2a$.

答案： 解：原式$=\left(\frac{(a-1)(a-5)}{a-5}-\frac{5}{a-5}\right)\cdot \frac{2(a-5)}{-(a-6)}$
$=\frac{a^{2}-6a+5 - 5}{a-5}\cdot \frac{2(a-5)}{-(a-6)}$
$=\frac{a^{2}-6a}{a-5}\cdot \frac{2(a-5)}{-(a-6)}$
$=\frac{a(a - 6)}{a-5}\cdot \frac{2(a-5)}{-(a - 6)}$
$=-2a$
故答案为：$-2a$

12. 化简：$\frac {2a}{a^{2}-4}-\frac {1}{a-2}= $$\frac{1}{a + 2}$.

答案： 解：$\frac{2a}{a^2 - 4} - \frac{1}{a - 2}$
$=\frac{2a}{(a + 2)(a - 2)} - \frac{a + 2}{(a + 2)(a - 2)}$
$=\frac{2a - (a + 2)}{(a + 2)(a - 2)}$
$=\frac{2a - a - 2}{(a + 2)(a - 2)}$
$=\frac{a - 2}{(a + 2)(a - 2)}$
$=\frac{1}{a + 2}$
$\frac{1}{a + 2}$

13. 若$(-\frac {x^{2}}{my})^{4}= \frac {x^{8}}{16y^{4}}(m＞0)$,则 m 的值为______2.

答案： 解：$(-\frac{x^{2}}{my})^{4} = \frac{(x^{2})^{4}}{(my)^{4}} = \frac{x^{8}}{m^{4}y^{4}}$
因为$\frac{x^{8}}{m^{4}y^{4}} = \frac{x^{8}}{16y^{4}}$，所以$m^{4} = 16$
解得$m = 2$（$m＞0$）
答案：2

14. 已知$\frac {A}{3x-2}-\frac {B}{2x+3}= \frac {2x+16}{(3x-2)(2x+3)}$,则 A,B 的值分别为4,2.

答案： 解：左边通分得：$\frac{A(2x+3)-B(3x-2)}{(3x-2)(2x+3)} = \frac{(2A - 3B)x + (3A + 2B)}{(3x-2)(2x+3)}$
由等式两边分子相等得：$\begin{cases}2A - 3B = 2 \\ 3A + 2B = 16\end{cases}$
解方程组：
由$2A - 3B = 2$得$2A = 3B + 2$，$A = \frac{3B + 2}{2}$
代入$3A + 2B = 16$：$3×\frac{3B + 2}{2} + 2B = 16$
$9B + 6 + 4B = 32$
$13B = 26$
$B = 2$
则$A = \frac{3×2 + 2}{2} = 4$
4，2

15. 已知$A= \frac {xy-y^{2}}{y^{2}-x^{2}}÷(\frac {1}{x-y}-\frac {1}{x+y})$.
(1)化简 A；
(2)当$x^{2}+y^{2}= 13,xy= -6$时,求 A 的值.

答案： 解：
(1) $ A = \frac { y ( x - y ) } { ( y - x ) ( y + x ) } ÷ ( \frac { x + y } { x ^ { 2 } - y ^ { 2 } } - \frac { x - y } { x ^ { 2 } - y ^ { 2 } } ) = - \frac { y } { x + y } \cdot \frac { ( x + y ) ( x - y ) } { 2 y } = \frac { y - x } { 2 } $
(2) 因为 $ x ^ { 2 } + y ^ { 2 } = 13 $，$ x y = - 6 $，所以 $ x ^ { 2 } - 2 x y + y ^ { 2 } = 25 $，所以 $ ( x - y ) ^ { 2 } = 25 $，所以 $ x - y = \pm 5 $，所以原式 $ = \pm \frac { 5 } { 2 } $

16. 化简$(\frac {x}{x+1}+\frac {x}{x-1})\cdot \frac {x^{2}-1}{x}$. 下面是甲、乙两位同学的部分运算过程：

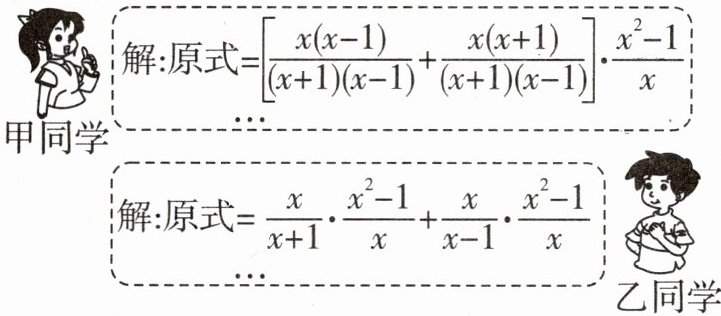
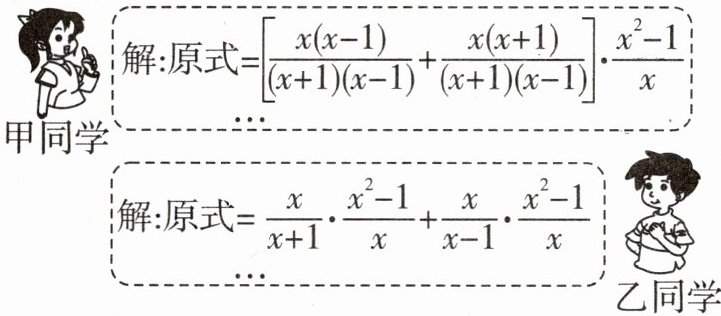
(1)甲同学的解法的依据是②,乙同学的解法的依据是③；(填序号)
①等式的基本性质；②分式的基本性质；③乘法分配律；④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
选择乙同学的解法：
解：原式$=\frac{x}{x+1}\cdot \frac{x^{2}-1}{x}+\frac{x}{x-1}\cdot \frac{x^{2}-1}{x}$
$=\frac{x}{x+1}\cdot \frac{(x+1)(x-1)}{x}+\frac{x}{x-1}\cdot \frac{(x+1)(x-1)}{x}$
$=x - 1 + x + 1$
$=2x$

答案：
(1) ② ③
(2) 选择乙同学的解法：
解：原式$=\frac{x}{x+1}\cdot \frac{x^{2}-1}{x}+\frac{x}{x-1}\cdot \frac{x^{2}-1}{x}$
$=\frac{x}{x+1}\cdot \frac{(x+1)(x-1)}{x}+\frac{x}{x-1}\cdot \frac{(x+1)(x-1)}{x}$
$=x - 1 + x + 1$
$=2x$

17. 已知代数式$A= \frac {3}{x+2},B= \frac {x-2}{x+3}÷\frac {x^{2}-4}{2x+6}-\frac {5}{x+2}$.
(1)试说明：若 A,B 均有意义,则它们的值互为相反数；
(2)若代数式 A,B 中的 x 是满足不等式$3(x-3)＜6-2x$的正整数解,求 A - B 的值.

答案： 解：
(1) 因为 $ A = \frac { 3 } { x + 2 } $，$ B = \frac { x - 2 } { x + 3 } ÷ \frac { x ^ { 2 } - 4 } { 2 x + 6 } - \frac { 5 } { x + 2 } $，所以 $ A + B = \frac { 3 } { x + 2 } + \frac { x - 2 } { x + 3 } ÷ \frac { x ^ { 2 } - 4 } { 2 x + 6 } - \frac { 5 } { x + 2 } = \frac { 3 } { x + 2 } + \frac { x - 2 } { x + 3 } \cdot \frac { 2 ( x + 3 ) } { ( x + 2 ) ( x - 2 ) } - \frac { 5 } { x + 2 } = \frac { 3 } { x + 2 } + \frac { 2 } { x + 2 } - \frac { 5 } { x + 2 } = \frac { 3 + 2 - 5 } { x + 2 } = 0 $。所以 $ A $，$ B $ 互为相反数。
(2) 由
(1)知 $ B = - \frac { 3 } { x + 2 } $，所以 $ A - B = \frac { 3 } { x + 2 } + \frac { 3 } { x + 2 } = \frac { 6 } { x + 2 } $。解不等式 $ 3 ( x - 3 ) ＜ 6 - 2 x $，得 $ x ＜ 3 $。因为 $ x $ 是满足不等式 $ 3 ( x - 3 ) ＜ 6 - 2 x $ 的正整数解，所以 $ x = 1 $ 或 $ x = 2 $(舍去)，所以当 $ x = 1 $ 时，原式 $ = \frac { 6 } { 1 + 2 } = 2 $。