《2025年假期伴你行暑假合肥工业大学出版社七年级数学沪科版》

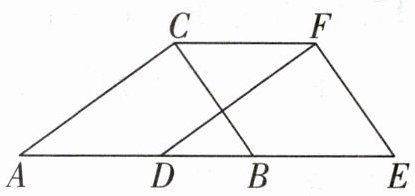
20. (10分)如图,在直角三角形ABC中,$∠ACB= 90^{\circ },AC= 4cm,BC= 3cm$,三角形ABC沿AB方向平移至三角形DEF,若$AE= 8cm,DB= 2cm.$
(1)求三角形ABC沿AB方向平移的距离；
(2)求四边形AEFC的周长.

答案： （1）因为三角形$ABC$沿$AB$方向平移至三角形$DEF$，所以$AD=BE=CF$。
已知$AE=8\ cm$，$DB=2\ cm$，且$AE=AD+DB+BE$，又因为$AD=BE$，设$AD=BE=x\ cm$，则$8=x+2+x$，解得$x=3$，所以平移距离$AD=3\ cm$。
（2）由平移性质得$CF=AD=3\ cm$，$EF=BC=3\ cm$。
四边形$AEFC$的周长为$AE+EF+CF+AC=8+3+3+4=18\ cm$。
答：（1）平移距离为$3\ cm$；（2）四边形$AEFC$的周长为$18\ cm$。

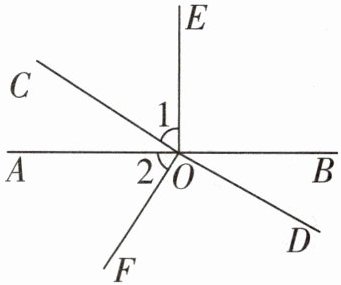
21. (12分)如图,直线AB,CD相交于点O,$OE⊥AB.$
(1)若$∠BOC= 4∠AOC$,求$∠BOD$的度数；
(2)若$∠1= ∠2$,OF⊥CD吗？请说明理由.

答案： （1）解：由邻补角的定义，得$∠AOC + ∠BOC = 180^{\circ}$。
因为$∠BOC = 4∠AOC$，所以$4∠AOC + ∠AOC = 180^{\circ}$，
解得$∠AOC = 36^{\circ}$。
由对顶角相等，得$∠BOD = ∠AOC = 36^{\circ}$。
（2）$OF⊥CD$。理由如下：
因为$OE⊥AB$，所以$∠AOE = 90^{\circ}$，即$∠1 + ∠AOC = 90^{\circ}$。
因为$∠1 = ∠2$，所以$∠2 + ∠AOC = 90^{\circ}$，即$∠FOC = 90^{\circ}$，
所以$OF⊥CD$。

22. (16分)如图,一副三角板的两个直角顶点重合在一起,交叉摆放.

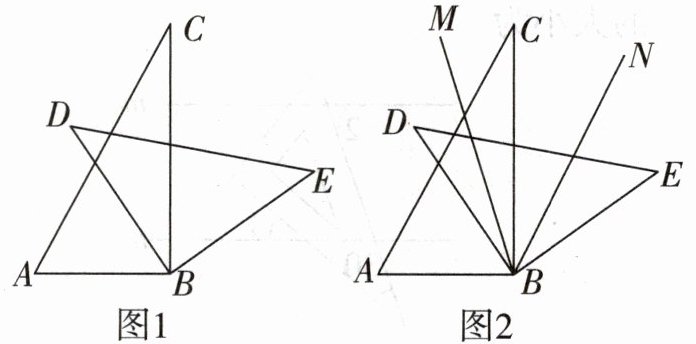
(1)如图1,若$∠CBD= 35^{\circ }$,则$∠ABE= $145$^{\circ }$；
(2)如图1,若$∠CBD= α$,求$∠ABE$的度数；
解：因为$∠ABC=90^{\circ}$，$∠CBD=\alpha$，所以$∠ABD=∠ABC - ∠CBD=90^{\circ}-\alpha$。因为$∠DBE=90^{\circ}$，所以$∠ABE=∠ABD + ∠DBE=90^{\circ}-\alpha + 90^{\circ}=180^{\circ}-\alpha$。
(3)如图2,射线BM,射线BN分别是$∠ABE和∠CBE$的平分线,试判断当$∠CBD$的度数改变时,$∠MBN$的度数是否随之改变. 若改变,请说明理由；若不改变,求它的度数.
解：不变，$∠MBN=45^{\circ}$。理由如下：由（2）知$∠ABE=180^{\circ}-\alpha$，因为$BM$平分$∠ABE$，所以$∠MBE=\frac{1}{2}∠ABE=\frac{1}{2}(180^{\circ}-\alpha)=90^{\circ}-\frac{\alpha}{2}$。因为$∠CBE=∠DBE - ∠CBD=90^{\circ}-\alpha$，$BN$平分$∠CBE$，所以$∠NBE=\frac{1}{2}∠CBE=\frac{1}{2}(90^{\circ}-\alpha)=45^{\circ}-\frac{\alpha}{2}$。所以$∠MBN=∠MBE - ∠NBE=(90^{\circ}-\frac{\alpha}{2})-(45^{\circ}-\frac{\alpha}{2})=45^{\circ}$。

答案： （1）145
（2）解：因为$∠ABC=90^{\circ}$，$∠CBD=\alpha$，所以$∠ABD=∠ABC - ∠CBD=90^{\circ}-\alpha$。因为$∠DBE=90^{\circ}$，所以$∠ABE=∠ABD + ∠DBE=90^{\circ}-\alpha + 90^{\circ}=180^{\circ}-\alpha$。
（3）解：不变，$∠MBN=45^{\circ}$。理由如下：由（2）知$∠ABE=180^{\circ}-\alpha$，因为$BM$平分$∠ABE$，所以$∠MBE=\frac{1}{2}∠ABE=\frac{1}{2}(180^{\circ}-\alpha)=90^{\circ}-\frac{\alpha}{2}$。因为$∠CBE=∠DBE - ∠CBD=90^{\circ}-\alpha$，$BN$平分$∠CBE$，所以$∠NBE=\frac{1}{2}∠CBE=\frac{1}{2}(90^{\circ}-\alpha)=45^{\circ}-\frac{\alpha}{2}$。所以$∠MBN=∠MBE - ∠NBE=(90^{\circ}-\frac{\alpha}{2})-(45^{\circ}-\frac{\alpha}{2})=45^{\circ}$。