第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
例 已知$∠AOB= 90^{\circ }$,OC是从$∠AOB$的顶点O引出的一条射线,若$∠AOB= 2∠BOC$,求$∠AOC$的度数。
错解 如图,因为$∠AOB= 90^{\circ }$,$∠AOB= 2∠BOC$,所以$∠BOC= 45^{\circ }$,所以$∠AOC= ∠AOB-∠BOC= 90^{\circ }-45^{\circ }=45^{\circ }$。
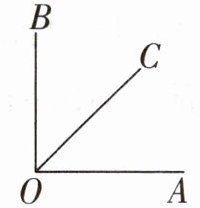
错因分析 射线OC需分在$∠AOB$的内部和外部两种情况。当OC在$∠AOB$的内部时,$∠AOC等于∠AOB与∠BOC$的差;当OC在$∠AOB$的外部时,$∠AOC等于∠AOB与∠BOC$的和。本题忽略了射线OC在$∠AOB$外部的情况,导致漏解。
正解 因为$∠AOB= 90^{\circ }$,$∠AOB= 2∠BOC$,所以$∠BOC= 45^{\circ }$。分以下两种情况:
①当OC在$∠AOB$的内部时(如图1),$∠AOC= ∠AOB-∠BOC= 90^{\circ }-45^{\circ }=45^{\circ }$;
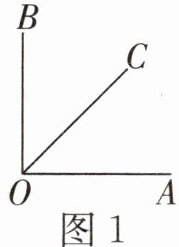
②当OC在$∠AOB$的外部时(如图2),$∠AOC= ∠AOB+∠BOC= 90^{\circ }+45^{\circ }=135^{\circ }$。
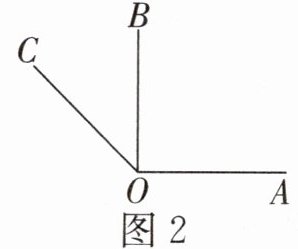
综上所述,$∠AOC的度数为45^{\circ }或135^{\circ }$。
错解 如图,因为$∠AOB= 90^{\circ }$,$∠AOB= 2∠BOC$,所以$∠BOC= 45^{\circ }$,所以$∠AOC= ∠AOB-∠BOC= 90^{\circ }-45^{\circ }=45^{\circ }$。

错因分析 射线OC需分在$∠AOB$的内部和外部两种情况。当OC在$∠AOB$的内部时,$∠AOC等于∠AOB与∠BOC$的差;当OC在$∠AOB$的外部时,$∠AOC等于∠AOB与∠BOC$的和。本题忽略了射线OC在$∠AOB$外部的情况,导致漏解。
正解 因为$∠AOB= 90^{\circ }$,$∠AOB= 2∠BOC$,所以$∠BOC= 45^{\circ }$。分以下两种情况:
①当OC在$∠AOB$的内部时(如图1),$∠AOC= ∠AOB-∠BOC= 90^{\circ }-45^{\circ }=45^{\circ }$;

②当OC在$∠AOB$的外部时(如图2),$∠AOC= ∠AOB+∠BOC= 90^{\circ }+45^{\circ }=135^{\circ }$。

综上所述,$∠AOC的度数为45^{\circ }或135^{\circ }$。
答案:
【解析】:
题目考查了角的计算,关键是要考虑到射线$OC$在$\angle AOB$内部和外部两种情况。
当$OC$在$\angle AOB$内部时,$\angle AOC$等于$\angle AOB$与$\angle BOC$的差;当$OC$在$\angle AOB$外部时,$\angle AOC$等于$\angle AOB$与$\angle BOC$的和。
【答案】:
因为$\angle AOB = 90^{\circ}$,$\angle AOB = 2\angle BOC$,所以$\angle BOC = 45^{\circ}$。
分以下两种情况:
①当$OC$在$\angle AOB$的内部时(如图1),$\angle AOC=\angle AOB - \angle BOC = 90^{\circ}-45^{\circ}=45^{\circ}$;
②当$OC$在$\angle AOB$的外部时(如图2),$\angle AOC=\angle AOB + \angle BOC = 90^{\circ}+45^{\circ}=135^{\circ}$。
综上所述,$\angle AOC$的度数为$45^{\circ}$或$135^{\circ}$。
题目考查了角的计算,关键是要考虑到射线$OC$在$\angle AOB$内部和外部两种情况。
当$OC$在$\angle AOB$内部时,$\angle AOC$等于$\angle AOB$与$\angle BOC$的差;当$OC$在$\angle AOB$外部时,$\angle AOC$等于$\angle AOB$与$\angle BOC$的和。
【答案】:
因为$\angle AOB = 90^{\circ}$,$\angle AOB = 2\angle BOC$,所以$\angle BOC = 45^{\circ}$。
分以下两种情况:
①当$OC$在$\angle AOB$的内部时(如图1),$\angle AOC=\angle AOB - \angle BOC = 90^{\circ}-45^{\circ}=45^{\circ}$;
②当$OC$在$\angle AOB$的外部时(如图2),$\angle AOC=\angle AOB + \angle BOC = 90^{\circ}+45^{\circ}=135^{\circ}$。
综上所述,$\angle AOC$的度数为$45^{\circ}$或$135^{\circ}$。
查看更多完整答案,请扫码查看


