《2025年假期伴你行暑假合肥工业大学出版社七年级数学沪科版》

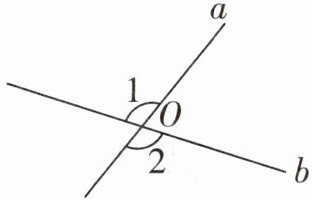
1. (桂林中考)如图,直线a,b相交于点O,∠1= 110°,则∠2的度数是 (C)

A.70°
B.90°
C.110°
D.130°

答案： 解：由图可知，∠1与∠2是对顶角。
因为对顶角相等，∠1=110°，
所以∠2=∠1=110°。
答案：C

2. (广西中考)已知∠1与∠2为对顶角,∠1= 35°,则∠2= ______°.
35

答案： 解：因为∠1与∠2为对顶角，根据对顶角相等的性质，可得∠2=∠1。已知∠1=35°，所以∠2=35°。
35

3. (西藏中考)如图,已知直线$l_1//l_2,AB⊥CD$于点D,∠1= 50°,则∠2的度数是 (A)
A.40°
B.45°
C.50°
D.60°

答案： 解：
∵直线$l_1//l_2$，$\angle1 = 50^{\circ}$
$\therefore\angle ABC=\angle1 = 50^{\circ}$（两直线平行，内错角相等）
∵$AB\perp CD$
$\therefore\angle BDC = 90^{\circ}$
在$\triangle BDC$中，$\angle2=180^{\circ}-\angle BDC-\angle ABC$
$=180^{\circ}-90^{\circ}-50^{\circ}$
$=40^{\circ}$
答案：A

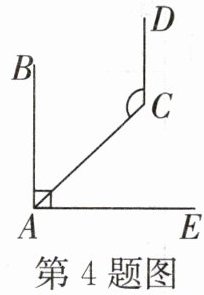
4. (益阳中考)如图,AB//CD,AB⊥AE,∠CAE= 42°,则∠ACD的度数为______.

132°

答案： 解：
∵AB⊥AE，
∴∠BAE=90°，
∵∠CAE=42°，
∴∠BAC=∠BAE - ∠CAE=90° - 42°=48°，
∵AB//CD，
∴∠BAC + ∠ACD=180°，
∴∠ACD=180° - ∠BAC=180° - 48°=132°。
故答案为：132°。

5. (贺州中考)如图,下列两个角是同旁内角的是 (B)
A.∠1与∠2
B.∠1与∠3
C.∠1与∠4
D.∠2与∠4

答案： 根据同旁内角的定义：两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角。观察图形可知：
- 直线a、b被直线c所截，∠1与∠3在截线c的同旁，且分别在直线a、b的内侧，符合同旁内角的定义。
- 选项A中∠1与∠2是内错角；选项C中∠1与∠4是对顶角；选项D中∠2与∠4是同位角。
答案：B

6. (百色中考)如图,与∠1是内错角的是(C)
A.∠2
B.∠3
C.∠4
D.∠5

答案： 根据内错角定义：两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角。
观察图形，∠1与∠4是直线a、b被直线c所截形成的内错角。
答案：C

7. (梧州中考)如图,已知直线a,b被直线c所截,下列条件不能判断a//b的是 (D)
A.∠2= ∠6
B.∠2+∠3= 180°
C.∠1= ∠4
D.∠5+∠6= 180°

答案： A.∠2与∠6是同位角，∠2=∠6，根据同位角相等，两直线平行，能判断a//b；
B.∠2与∠3是同旁内角，∠2+∠3=180°，根据同旁内角互补，两直线平行，能判断a//b；
C.∠1与∠4是内错角，∠1=∠4，根据内错角相等，两直线平行，能判断a//b；
D.∠5与∠6是邻补角，∠5+∠6=180°恒成立，不能判断a//b。
答案：D

8. (泰州中考)如图,木棒AB,CD与EF分别在点G,H处用可旋转的螺丝铆住,∠EGB= 100°,∠EHD= 80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转20°.

答案： 解：因为∠EHD=80°，所以∠CHG=∠EHD=80°（对顶角相等）。
当AB绕点G逆时针旋转到与CD平行时，设旋转后AB的位置为AB'，则AB'//CD。
此时∠EGB'=∠CHG=80°（两直线平行，同位角相等）。
因为∠EGB=100°，所以旋转角为∠BGB'=∠EGB - ∠EGB'=100° - 80°=20°。
故至少要旋转20°。
答案：20

9. (兰州中考)将一副三角板如图摆放,则BC//ED,理由是内错角相等，两直线平行.

答案： BC ED 内错角相等，两直线平行

10. (湘潭中考)如图,点E是AD延长线上一点,如果添加一个条件,使BC//AD,则可添加的条件为$ \angle A + \angle ABC = 180^{\circ} $（或$ \angle C + \angle ADC = 180^{\circ} $或$ \angle CBD = \angle ADB $或$ \angle C = \angle CDE $）. (任意添加一个符合题意的条件即可)

答案： $ \angle A + \angle ABC = 180^{\circ} $（或$ \angle C + \angle ADC = 180^{\circ} $或$ \angle CBD = \angle ADB $或$ \angle C = \angle CDE $）

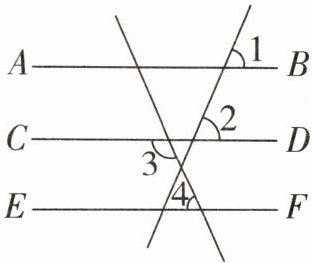
11. (成都模拟)如图,已知∠1= ∠2,∠3+∠4= 180°,试说明:AB//EF.

答案： 解：因为∠1=∠2，所以AB//CD（同位角相等，两直线平行）。
因为∠3+∠4=180°，所以CD//EF（同旁内角互补，两直线平行）。
所以AB//EF（平行于同一条直线的两条直线平行）。