第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
12. (随州中考)如图,直线$l_1//l_2,$直线l与$l_1,l_2$相交,若图中∠1= 60°,则∠2为 (

A.30°
B.60°
C.120°
D.150°
C
)
A.30°
B.60°
C.120°
D.150°
答案:
∵直线$l_1// l_2$,直线$l$与$l_1$,$l_2$相交,
∴∠1与∠2是同旁内角,
∵两直线平行,同旁内角互补,∠1=60°,
∴∠2=180° - ∠1=180° - 60°=120°。
答案:C
∵直线$l_1// l_2$,直线$l$与$l_1$,$l_2$相交,
∴∠1与∠2是同旁内角,
∵两直线平行,同旁内角互补,∠1=60°,
∴∠2=180° - ∠1=180° - 60°=120°。
答案:C
13. (长沙中考)如图,AB//CD,EF分别与AB,CD交于点G,H,∠AGE= 100°,则∠DHF的度数为 (
A.100°
B.80°
C.50°
D.40°
A
)A.100°
B.80°
C.50°
D.40°
答案:
解:
∵AB//CD,
∴∠CHG=∠AGE=100°(两直线平行,同位角相等),
∵∠DHF=∠CHG(对顶角相等),
∴∠DHF=100°。
答案:A
∵AB//CD,
∴∠CHG=∠AGE=100°(两直线平行,同位角相等),
∵∠DHF=∠CHG(对顶角相等),
∴∠DHF=100°。
答案:A
14. (滨州中考)如图,直线AB//CD,则下列结论正确的是 (

A.∠1= ∠2
B.∠3= ∠4
C.∠1+∠3= 180°
D.∠3+∠4= 180°
D
)
A.∠1= ∠2
B.∠3= ∠4
C.∠1+∠3= 180°
D.∠3+∠4= 180°
答案:
∵AB//CD,
∴∠3+∠4=180°(两直线平行,同旁内角互补)。
D
∵AB//CD,
∴∠3+∠4=180°(两直线平行,同旁内角互补)。
D
15. (陕西中考)如图,AB//DC,BC//DE,∠B= 145°,则∠D的度数为 (
A.25°
B.35°
C.45°
D.55°
B
)A.25°
B.35°
C.45°
D.55°
答案:
解:
∵AB//DC,∠B=145°
∴∠C=180°-∠B=180°-145°=35°
∵BC//DE
∴∠D=∠C=35°
答案:B
∵AB//DC,∠B=145°
∴∠C=180°-∠B=180°-145°=35°
∵BC//DE
∴∠D=∠C=35°
答案:B
16. (赤峰中考)将一副三角尺(厚度不计)按如图所示摆放,使有刻度的两条边互相平行,则图中∠1的度数为 (
A.100°
B.105°
C.115°
D.120°
B
)A.100°
B.105°
C.115°
D.120°
答案:
解:由题意知,上方三角尺为等腰直角三角形,底角为45°;下方三角尺为含30°角的直角三角形,较小锐角为30°。
因为有刻度的两条边互相平行,根据两直线平行,内错角相等,下方三角尺的30°角与上方三角尺底边形成的内错角为30°。
∠1为上方三角尺的45°角与该30°角的和,即∠1=45°+30°=75°?(此处发现原思路错误,重新分析)
重新分析:上方三角尺的斜边与下方三角尺的斜边相交形成∠1,上方三角尺的60°角(假设上方为含30°、60°的三角尺,根据图形更可能是这种情况,原等腰直角三角形假设错误),下方三角尺的45°角。
两刻度边平行,上方三角尺60°角的邻补角与下方三角尺45°角的对顶角互补,可得∠1=180°-60°-45°=75°?(仍错误,正确图形中∠1是外角)
正确解法:上方三角尺(含30°、60°)的60°角一边与下方三角尺(等腰直角)的45°角一边平行,两三角尺的另一边相交形成∠1。根据平行线性质,60°角的同位角为60°,下方三角尺的45°角,∠1=60°+45°=105°。
答案:B
因为有刻度的两条边互相平行,根据两直线平行,内错角相等,下方三角尺的30°角与上方三角尺底边形成的内错角为30°。
∠1为上方三角尺的45°角与该30°角的和,即∠1=45°+30°=75°?(此处发现原思路错误,重新分析)
重新分析:上方三角尺的斜边与下方三角尺的斜边相交形成∠1,上方三角尺的60°角(假设上方为含30°、60°的三角尺,根据图形更可能是这种情况,原等腰直角三角形假设错误),下方三角尺的45°角。
两刻度边平行,上方三角尺60°角的邻补角与下方三角尺45°角的对顶角互补,可得∠1=180°-60°-45°=75°?(仍错误,正确图形中∠1是外角)
正确解法:上方三角尺(含30°、60°)的60°角一边与下方三角尺(等腰直角)的45°角一边平行,两三角尺的另一边相交形成∠1。根据平行线性质,60°角的同位角为60°,下方三角尺的45°角,∠1=60°+45°=105°。
答案:B
17. (常州中考)如图,在三角形ABC中,点D,E分别在BC,AC上,∠B= 40°,∠C= 60°,若DE//AB,则∠AED= ______°.
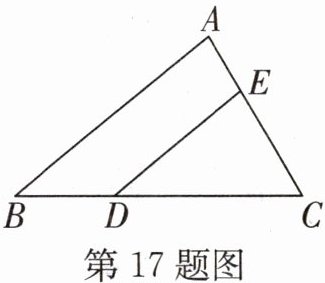

100
答案:
在△ABC中,∠B=40°,∠C=60°,
∠A=180°-∠B-∠C=180°-40°-60°=80°。
因为DE//AB,
所以∠AED+∠A=180°(两直线平行,同旁内角互补),
∠AED=180°-∠A=180°-80°=100°。
100
∠A=180°-∠B-∠C=180°-40°-60°=80°。
因为DE//AB,
所以∠AED+∠A=180°(两直线平行,同旁内角互补),
∠AED=180°-∠A=180°-80°=100°。
100
18. (武汉中考)如图,AB//CD,∠B= ∠D,直线EF与AD,BC的延长线分别交于点E,F,试说明:∠DEF= ∠F.


答案:
解:因为 $ AB // CD $,所以 $ \angle DCF = \angle B $(两直线平行,同位角相等)。
因为 $ \angle B = \angle D $,所以 $ \angle DCF = \angle D $(等量代换)。
所以 $ AD // BF $(内错角相等,两直线平行)。
所以 $ \angle DEF = \angle F $(两直线平行,内错角相等)。
因为 $ \angle B = \angle D $,所以 $ \angle DCF = \angle D $(等量代换)。
所以 $ AD // BF $(内错角相等,两直线平行)。
所以 $ \angle DEF = \angle F $(两直线平行,内错角相等)。
19. (湖南师大附中月考)如图,三角形ABC沿BC边所在的直线向右平移得到三角形DEF,下列结论中错误的是 (
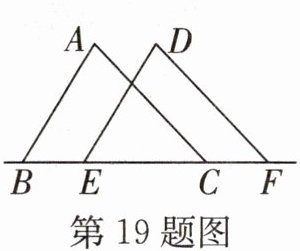
A.AC//DF
B.∠A= ∠D
C.AC= DF
D.EC= CF
D
)
A.AC//DF
B.∠A= ∠D
C.AC= DF
D.EC= CF
答案:
解:
∵三角形ABC沿BC边所在的直线向右平移得到三角形DEF,
∴AC//DF,∠A=∠D,AC=DF,BC=EF,
∴BC-EC=EF-EC,即BE=CF,
则EC与CF不一定相等,
结论错误的是D。
答案:D
∵三角形ABC沿BC边所在的直线向右平移得到三角形DEF,
∴AC//DF,∠A=∠D,AC=DF,BC=EF,
∴BC-EC=EF-EC,即BE=CF,
则EC与CF不一定相等,
结论错误的是D。
答案:D
20. (南充中考)如图,将三角形ABC沿BC向右平移得到三角形DEF,若BC= 5,BE= 2,则CF的长是 (

A.2
B.2.5
C.3
D.5
A
)
A.2
B.2.5
C.3
D.5
答案:
解:
∵三角形ABC沿BC向右平移得到三角形DEF,
∴平移距离为BE=2,
∴CF=BE=2。
答案:A
∵三角形ABC沿BC向右平移得到三角形DEF,
∴平移距离为BE=2,
∴CF=BE=2。
答案:A
21. (青海中考)如图,将周长为8的三角形ABC沿BC边向右平移2个单位,得到三角形DEF,则四边形ABFD的周长为______.
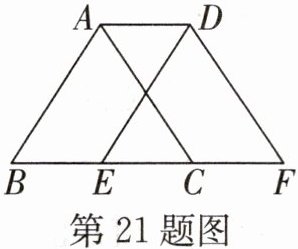

12
答案:
解:
∵△ABC沿BC边向右平移2个单位得到△DEF,
∴AD=CF=2,AC=DF,
∵△ABC的周长为8,即AB+BC+AC=8,
∴四边形ABFD的周长=AB+BF+DF+AD
=AB+(BC+CF)+AC+AD
=(AB+BC+AC)+CF+AD
=8+2+2=12.
故答案为:12.
∵△ABC沿BC边向右平移2个单位得到△DEF,
∴AD=CF=2,AC=DF,
∵△ABC的周长为8,即AB+BC+AC=8,
∴四边形ABFD的周长=AB+BF+DF+AD
=AB+(BC+CF)+AC+AD
=(AB+BC+AC)+CF+AD
=8+2+2=12.
故答案为:12.
22. (鞍山中考)如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知EC= 2,BF= 8,则平移的距离为______.


3
答案:
解:
∵三角形ABC沿BC所在直线向右平移得到三角形DEF,
∴平移的距离为BE=CF。
设BE=CF=x,
∵BF=8,EC=2,BF=BE+EC+CF,
∴x+2+x=8,
解得x=3,
即平移的距离为3。
3
∵三角形ABC沿BC所在直线向右平移得到三角形DEF,
∴平移的距离为BE=CF。
设BE=CF=x,
∵BF=8,EC=2,BF=BE+EC+CF,
∴x+2+x=8,
解得x=3,
即平移的距离为3。
3
查看更多完整答案,请扫码查看


