第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
26. (4分)已知$2 a - 1的平方根是\pm 3 , 3 a + b - 1$的算术平方根是4,求$50 a - 17 b$的立方根。
答案:
解:因为$2a - 1$的平方根是$\pm 3$,所以$2a - 1 = (\pm 3)^2 = 9$,解得$a = 5$。
因为$3a + b - 1$的算术平方根是$4$,所以$3a + b - 1 = 4^2 = 16$。将$a = 5$代入,得$3×5 + b - 1 = 16$,即$15 + b - 1 = 16$,解得$b = 2$。
所以$50a - 17b = 50×5 - 17×2 = 250 - 34 = 216$。
因为$216$的立方根是$\sqrt[3]{216} = 6$,所以$50a - 17b$的立方根是$6$。
因为$3a + b - 1$的算术平方根是$4$,所以$3a + b - 1 = 4^2 = 16$。将$a = 5$代入,得$3×5 + b - 1 = 16$,即$15 + b - 1 = 16$,解得$b = 2$。
所以$50a - 17b = 50×5 - 17×2 = 250 - 34 = 216$。
因为$216$的立方根是$\sqrt[3]{216} = 6$,所以$50a - 17b$的立方根是$6$。
27. (5分)如图,一只蚂蚁从点$A$沿数轴向右爬2个单位长度到达点$B$,点$A表示- \sqrt { 2 }$,设点$B所表示的数为m$。
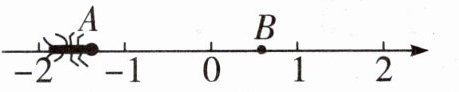
(1)求$m$的值;
(2)求$| m - 1 |$的值。
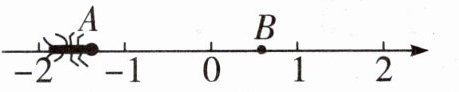
(1)求$m$的值;
(2)求$| m - 1 |$的值。
答案:
解:
(1) 因为蚂蚁从点A沿数轴向右爬2个单位长度到达点B,点A表示$-\sqrt{2}$,所以$m = -\sqrt{2} + 2$。
(2) 由
(1)知$m = -\sqrt{2} + 2$,则$|m - 1| = |-\sqrt{2} + 2 - 1| = |-\sqrt{2} + 1| = \sqrt{2} - 1$。
(1) 因为蚂蚁从点A沿数轴向右爬2个单位长度到达点B,点A表示$-\sqrt{2}$,所以$m = -\sqrt{2} + 2$。
(2) 由
(1)知$m = -\sqrt{2} + 2$,则$|m - 1| = |-\sqrt{2} + 2 - 1| = |-\sqrt{2} + 1| = \sqrt{2} - 1$。
28. (6分)我们知道,负数没有算术平方根,但对于三个互不相等的负整数,若两两乘积的算术平方根都是整数,则称这三个数为“完美组合数”。例如:-18,-2,-8这三个数,$\sqrt { ( - 18 ) × ( - 2 ) } = 6 , \sqrt { ( - 18 ) × ( - 8 ) } = 12 , \sqrt { ( - 8 ) × ( - 2 ) } = 4$,其结果6,12,4都是整数,所以-18,-2,-8这三个数称为“完美组合数”。
(1)-9,-4,-1这三个数是“完美组合数”吗?请说明理由;
(2)若三个数-6,-24,$a$是“完美组合数”,其中有两个数乘积的算术平方根为24.求$a$的值。
(1)-9,-4,-1这三个数是“完美组合数”吗?请说明理由;
(2)若三个数-6,-24,$a$是“完美组合数”,其中有两个数乘积的算术平方根为24.求$a$的值。
答案:
(1) 是,理由如下:
$\sqrt{(-9)×(-4)}=\sqrt{36}=6$,$\sqrt{(-9)×(-1)}=\sqrt{9}=3$,$\sqrt{(-4)×(-1)}=\sqrt{4}=2$,
6,3,2都是整数,所以-9,-4,-1是“完美组合数”。
(2) 分两种情况:
① 若$\sqrt{(-6)×a}=24$,则$(-6)×a=24^2=576$,解得$a=-96$。
验证:$\sqrt{(-6)×(-24)}=12$,$\sqrt{(-24)×(-96)}=48$,12,24,48都是整数,符合题意。
② 若$\sqrt{(-24)×a}=24$,则$(-24)×a=24^2=576$,解得$a=-24$,与-24重复,舍去。
综上,$a=-96$。
(1) 是,理由如下:
$\sqrt{(-9)×(-4)}=\sqrt{36}=6$,$\sqrt{(-9)×(-1)}=\sqrt{9}=3$,$\sqrt{(-4)×(-1)}=\sqrt{4}=2$,
6,3,2都是整数,所以-9,-4,-1是“完美组合数”。
(2) 分两种情况:
① 若$\sqrt{(-6)×a}=24$,则$(-6)×a=24^2=576$,解得$a=-96$。
验证:$\sqrt{(-6)×(-24)}=12$,$\sqrt{(-24)×(-96)}=48$,12,24,48都是整数,符合题意。
② 若$\sqrt{(-24)×a}=24$,则$(-24)×a=24^2=576$,解得$a=-24$,与-24重复,舍去。
综上,$a=-96$。
29. (9分)阅读下面的文字,解答问题:
大家知道$\sqrt { 2 }$是无理数,而无理数是无限不循环小数,因此$\sqrt { 2 }$的小数部分我们不可能全部写出来,于是小明用$\sqrt { 2 } - 1来表示\sqrt { 2 }$的小数部分。因为$\sqrt { 2 }$的整数部分是1,将这个数减去其整数部分,差就是小数部分。
请解答:
(1)$\sqrt { 17 }$的整数部分是
(2)如果$\sqrt { 5 }的小数部分为a , \sqrt { 13 }的整数部分为b$,求$a + b - \sqrt { 5 }$的值;
解:因为$2<\sqrt{5}<3$,所以$a=\sqrt{5}-2$。
因为$3<\sqrt{13}<4$,所以$b=3$。
所以$a+b-\sqrt{5}=\sqrt{5}-2+3-\sqrt{5}=1$。
(3)已知$10 + \sqrt { 3 } = x + y$,其中$x$是整数,且$0 < y < 1$,求$x - y$的相反数。
解:因为$1<3<4$,所以$1<\sqrt{3}<2$,所以$11<10+\sqrt{3}<12$。
因为$10+\sqrt{3}=x+y$,其中$x$是整数,且$0<y<1$,所以$x=11$,$y=10+\sqrt{3}-11=\sqrt{3}-1$。
所以$x-y=11-(\sqrt{3}-1)=12-\sqrt{3}$,所以$x-y$的相反数是$-12+\sqrt{3}$。
大家知道$\sqrt { 2 }$是无理数,而无理数是无限不循环小数,因此$\sqrt { 2 }$的小数部分我们不可能全部写出来,于是小明用$\sqrt { 2 } - 1来表示\sqrt { 2 }$的小数部分。因为$\sqrt { 2 }$的整数部分是1,将这个数减去其整数部分,差就是小数部分。
请解答:
(1)$\sqrt { 17 }$的整数部分是
4
,小数部分是$\sqrt{17}-4$
;(2)如果$\sqrt { 5 }的小数部分为a , \sqrt { 13 }的整数部分为b$,求$a + b - \sqrt { 5 }$的值;
解:因为$2<\sqrt{5}<3$,所以$a=\sqrt{5}-2$。
因为$3<\sqrt{13}<4$,所以$b=3$。
所以$a+b-\sqrt{5}=\sqrt{5}-2+3-\sqrt{5}=1$。
(3)已知$10 + \sqrt { 3 } = x + y$,其中$x$是整数,且$0 < y < 1$,求$x - y$的相反数。
解:因为$1<3<4$,所以$1<\sqrt{3}<2$,所以$11<10+\sqrt{3}<12$。
因为$10+\sqrt{3}=x+y$,其中$x$是整数,且$0<y<1$,所以$x=11$,$y=10+\sqrt{3}-11=\sqrt{3}-1$。
所以$x-y=11-(\sqrt{3}-1)=12-\sqrt{3}$,所以$x-y$的相反数是$-12+\sqrt{3}$。
答案:
(1) 4;$\sqrt{17}-4$
(2) 解:因为$2<\sqrt{5}<3$,所以$a=\sqrt{5}-2$。
因为$3<\sqrt{13}<4$,所以$b=3$。
所以$a+b-\sqrt{5}=\sqrt{5}-2+3-\sqrt{5}=1$。
(3) 解:因为$1<3<4$,所以$1<\sqrt{3}<2$,所以$11<10+\sqrt{3}<12$。
因为$10+\sqrt{3}=x+y$,其中$x$是整数,且$0<y<1$,所以$x=11$,$y=10+\sqrt{3}-11=\sqrt{3}-1$。
所以$x-y=11-(\sqrt{3}-1)=12-\sqrt{3}$,所以$x-y$的相反数是$-12+\sqrt{3}$。
(1) 4;$\sqrt{17}-4$
(2) 解:因为$2<\sqrt{5}<3$,所以$a=\sqrt{5}-2$。
因为$3<\sqrt{13}<4$,所以$b=3$。
所以$a+b-\sqrt{5}=\sqrt{5}-2+3-\sqrt{5}=1$。
(3) 解:因为$1<3<4$,所以$1<\sqrt{3}<2$,所以$11<10+\sqrt{3}<12$。
因为$10+\sqrt{3}=x+y$,其中$x$是整数,且$0<y<1$,所以$x=11$,$y=10+\sqrt{3}-11=\sqrt{3}-1$。
所以$x-y=11-(\sqrt{3}-1)=12-\sqrt{3}$,所以$x-y$的相反数是$-12+\sqrt{3}$。
查看更多完整答案,请扫码查看


