《2025年假期伴你行暑假合肥工业大学出版社七年级数学沪科版》

1. 下列图形中可以由一个基础图形通过平移变换得到的是(B)

答案： 解：平移变换不改变图形的形状、大小和方向，只改变图形的位置。观察各选项：
- A 图形需通过旋转得到，不符合平移特征；
- B 图形可由一个基础六边形通过平移得到，符合题意；
- C 图形需通过旋转或对称得到，不符合平移特征；
- D 图形需通过旋转得到，不符合平移特征。
结论：B

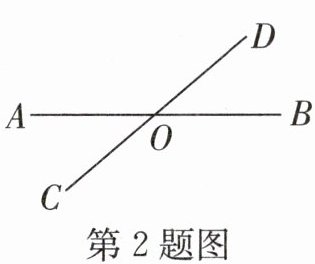
2. 如图,直线AB,CD相交于点O,$\angle AOD= 140^{\circ }$,则$\angle AOC$的度数是(A)

A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$70^{\circ }$

答案： 解：因为直线AB，CD相交于点O，
所以∠AOD与∠AOC互为邻补角，即∠AOD + ∠AOC = 180°。
已知∠AOD = 140°，
所以∠AOC = 180° - ∠AOD = 180° - 140° = 40°。
答案：A

3. 某同学的作业如下,其中※处填的依据是(C)
如图,已知直线$l_{1},l_{2},l_{3},l_{4}.$
若$∠1= ∠2$,则$∠3= ∠4.$
请完成下面的说理过程.
解：已知$∠1= ∠2,$
根据(内错角相等,两直线平行),得$l_{1}// l_{2}.$
再根据(※),得$∠3= ∠4.$

A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,同旁内角互补

答案： 解：已知$∠1 = ∠2$，
根据（内错角相等，两直线平行），得$l_{1}// l_{2}$。
再根据（两直线平行，同位角相等），得$∠3 = ∠4$。
答案：C

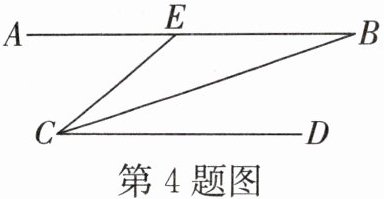
4. 如图,$AB// CD,∠AEC= 40^{\circ },CB平分∠DCE$,则$∠ABC$的度数为(B)

A.$10^{\circ }$
B.$20^{\circ }$
C.$30^{\circ }$
D.$40^{\circ }$

答案： 解：
∵AB//CD
∴∠AEC=∠ECD=40°（两直线平行，内错角相等）
∵CB平分∠DCE
∴∠BCD=∠ECD/2=40°/2=20°
∵AB//CD
∴∠ABC=∠BCD=20°（两直线平行，内错角相等）
答案：B

5. 如图,三角形ABC经过平移得到三角形DEF,其中点A的对应点是点D,则下列结论不一定正确的是(D)
A.$BC// EF$
B.$AD= BE$
C.$BE// CF$
D.$AC= EF$

答案： 解：根据平移性质，平移后对应边平行且相等，对应点连线平行且相等。
- A. BC与EF是对应边，所以BC//EF，正确。
- B. AD、BE是对应点连线，所以AD=BE，正确。
- C. BE、CF是对应点连线，所以BE//CF，正确。
- D. AC的对应边是DF，EF是BC的对应边，AC与EF不一定相等，错误。
结论：D

6. 如图是某机械加工厂加工的一种零件的示意图,其中$AB// CD,DE⊥BC,∠ABC= 70^{\circ }$,则$∠EDC$等于(B)
A.$10^{\circ }$
B.$20^{\circ }$
C.$30^{\circ }$
D.$40^{\circ }$

答案： 解：因为 $AB // CD$，所以 $\angle ABC = \angle BCD$（两直线平行，内错角相等）。
已知 $\angle ABC = 70^\circ$，故 $\angle BCD = 70^\circ$。
因为 $DE \perp BC$，所以 $\angle DEC = 90^\circ$（垂直定义）。
在 $\triangle DEC$ 中，$\angle EDC = 180^\circ - \angle DEC - \angle BCD = 180^\circ - 90^\circ - 70^\circ = 20^\circ$。
答案：B

7. 如图,直线$l_{1}和l_{2}被直线l_{3}和l_{4}$所截,$∠1= ∠2= 130^{\circ },∠3= 75^{\circ }$,则$∠4$的度数为(B)
A.$75^{\circ }$
B.$105^{\circ }$
C.$115^{\circ }$
D.$130^{\circ }$

答案： 解：
∵∠1=∠2=130°，
∴l₁//l₂（同位角相等，两直线平行）。
∵l₁//l₂，
∴∠3+∠4=180°（两直线平行，同旁内角互补）。
∵∠3=75°，
∴∠4=180°-∠3=180°-75°=105°。
答案：B

8. 如图,下列能判定$AB// EF$的条件有(C)
A.1个
B.2个
C.3个
D.4个

答案： ①
∵∠B+∠BFE=180°，
∴AB//EF（同旁内角互补，两直线平行）；
②
∵∠1=∠2，
∴DE//BC（内错角相等，两直线平行），无法判定AB//EF；
③
∵∠3=∠4，
∴AB//EF（内错角相等，两直线平行）；
④
∵∠B=∠5，
∴AB//EF（同位角相等，两直线平行）。
能判定AB//EF的条件有①③④，共3个。
答案：C

9. 如图,已知$∠1= ∠2= ∠3= 50^{\circ }$,则$∠4$的度数是(C)
A.$120^{\circ }$
B.$125^{\circ }$
C.$130^{\circ }$
D.$135^{\circ }$

答案： 解：
∵∠1=∠3=50°，
∴a//b（同位角相等，两直线平行）。
∵a//b，
∴∠2+∠5=180°（两直线平行，同旁内角互补）。
∵∠2=50°，
∴∠5=180°-50°=130°。
∵∠4=∠5（对顶角相等），
∴∠4=130°。
答案：C