《2025年暑假作业本大象出版社七年级数学华师大版》

5. 如图9-33,在折纸活动中,小明制作了一张$△ABC$纸片,点D,E分别在边AB,AC上,将$△ABC$沿着DE折叠压平,A与$A'$重合,若$∠A= 65^{\circ }$,则$∠1+∠2$的度数为 ( )


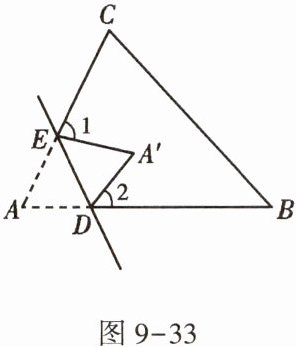
A.$130^{\circ }$
B.$210^{\circ }$
C.$105^{\circ }$
D.$75^{\circ }$

答案： A 提示：
∵ △A'DE 是 △ADE 翻折变换而成，
∴ ∠AED = ∠A'ED，∠ADE = ∠A'DE，∠A = ∠A' = 65°。
∴ ∠AED + ∠ADE = ∠A'ED + ∠A'DE = 180° - 65° = 115°。
∴ ∠1 + ∠2 = 360° - 2×115° = 130°。

6. 如图9-34,将$△ABC$绕点B逆时针旋转α,得到$△EBD$,若点A恰好在ED的延长线上,则$∠CAD$的度数为 ( )


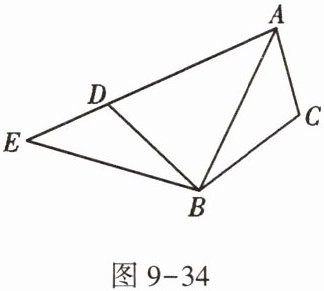
A.$90^{\circ }-α$
B.α
C.$180^{\circ }-α$
D.2α

答案： C 提示：由题意，得 ∠CBD = α，∠ACB = ∠EDB。
∵ ∠EDB + ∠ADB = 180°，
∴ ∠ADB + ∠ACB = 180°。
∵ ∠ADB + ∠CBD + ∠ACB + ∠CAD = 360°，∠CBD = α，
∴ ∠CAD = 180° - α。

7. 在如图9-35所示的方格纸(1格长为1个单位长度)中,$△ABC$的顶点都在格点上,将$△ABC$绕点O按顺时针方向旋转得到$△A'B'C'$,使各顶点仍在格点上,则其旋转角的度数是 _ .

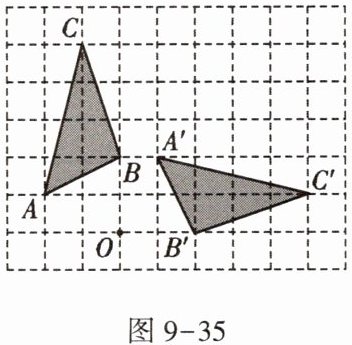
答案： 90°

8. 如图9-36,$△ABD$沿BD平移到了$△FCE$的位置,$BE= 10,CD= 4$,则平移的距离是 _ .

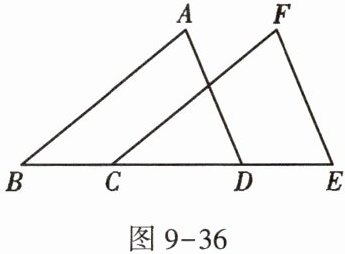
答案： 3

9. 有两个边长为4 cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图9-37中阴影部分的面积是 _ $cm^{2}$.

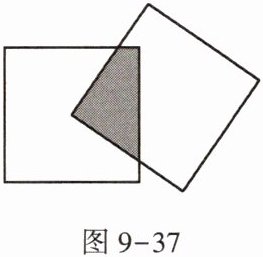
答案： 4

10. 如图9-38,将长方形ABCD绕点A顺时针旋转到长方形$AB'C'D'$的位置,旋转角为$α(0＜α＜90^{\circ })$.若$∠1= 110^{\circ }$,则$α=$ _ .

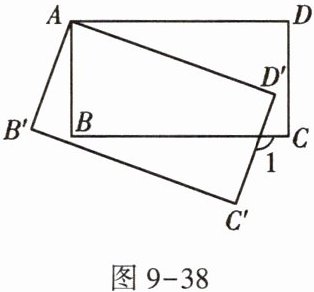
答案：
20° 提示：如图，
∵ 四边形 ABCD 为长方形，
∴ ∠B = ∠D = ∠BAD = 90°。

∵ 长方形 ABCD 绕点 A 顺时针旋转 α 得到长方形 AB'C'D'，
∴ ∠D' = ∠D = 90°，∠4 = α。
∵ ∠1 = ∠2 = 110°，
∴ ∠3 = 360° - 90° - 90° - 110° = 70°。
∴ ∠4 = 90° - 70° = 20°。
∴ α = 20°。