《2025年暑假作业本大象出版社七年级数学华师大版》

5. 认真阅读下面关于三角形内外角平分线所夹角的探究过程,完成所提出的问题.
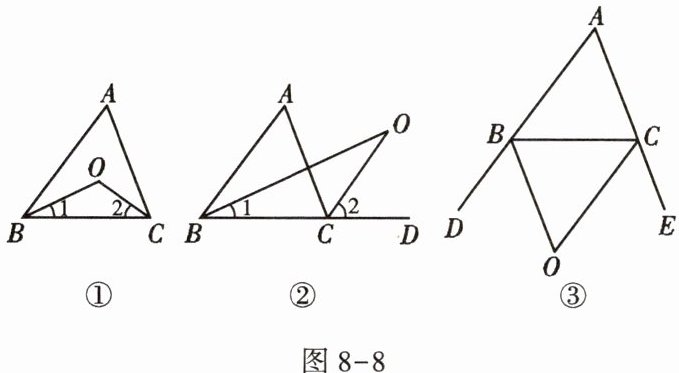
探究$1$：如图$8 - 8$①,在$\triangle ABC$中,$O是\angle ABC与\angle ACB的平分线BO和CO$的交点,通过分析发现$\angle BOC = 90^{\circ}+\frac{1}{2}\angle A$,理由如下.

$\because BO和CO分别是\angle ABC和\angle ACB$的平分线,
$\therefore \angle 1= \frac{1}{2}\angle ABC$,$\angle 2= \frac{1}{2}\angle ACB$.
$\therefore \angle 1+\angle 2= \frac{1}{2}(\angle ABC+\angle ACB)$.
又$\because \angle ABC+\angle ACB = 180^{\circ}-\angle A$,
$\therefore \angle 1+\angle 2= \frac{1}{2}(180^{\circ}-\angle A)= 90^{\circ}-\frac{1}{2}\angle A$.
$\therefore \angle BOC = 180^{\circ}-(\angle 1+\angle 2)= 180^{\circ}-(90^{\circ}-\frac{1}{2}\angle A)= 90^{\circ}+\frac{1}{2}\angle A$.
(1)探究$2$：如图$8 - 8$②,$O是\angle ABC与外角\angle ACD的平分线BO和CO$的交点,试分析$\angle BOC与\angle A$有怎样的关系,请说明理由.
(2)探究$3$：如图$8 - 8$③,$O是外角\angle DBC与外角\angle ECB的平分线BO和CO$的交点,则$\angle BOC与\angle A$有怎样的关系？(只写结论,不需证明)

答案：
(1) $ ∠BOC = \frac{1}{2}∠A $。理由如下：
∵ BO 和 CO 分别是 $ ∠ABC $ 和 $ ∠ACD $ 的平分线，
∴ $ ∠1 = \frac{1}{2}∠ABC $，$ ∠2 = \frac{1}{2}∠ACD $。
又
∵ $ ∠ACD $ 是 $ △ABC $ 的一外角，
∴ $ ∠ACD = ∠A + ∠ABC $。
∴ $ ∠2 = \frac{1}{2}(∠A + ∠ABC) = \frac{1}{2}∠A + ∠1 $。
∵ $ ∠2 $ 是 $ △BOC $ 的一外角，
∴ $ ∠BOC = ∠2 - ∠1 = \frac{1}{2}∠A + ∠1 - ∠1 = \frac{1}{2}∠A $。
(2) $ ∠BOC = 90° - \frac{1}{2}∠A $。