13. 某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话(图7-7):
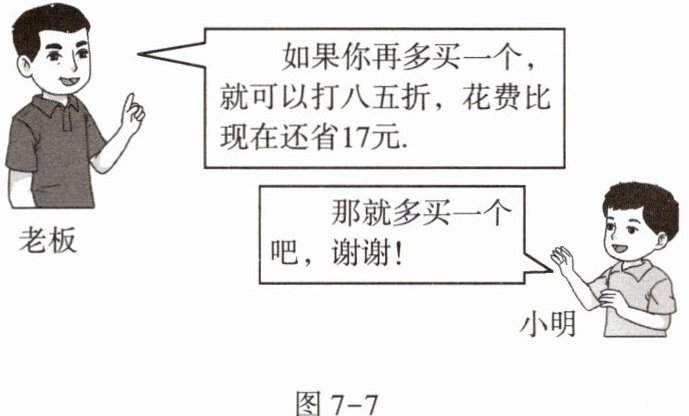
(1) 结合两人的对话内容,求小明原计划购买文具袋多少个.
(2) 学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元,其中钢笔标价每支8元,签字笔标价每支6元.经过沟通,这次老板给予八折优惠,那么小明最多可购买钢笔多少支?

(1) 结合两人的对话内容,求小明原计划购买文具袋多少个.
(2) 学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元,其中钢笔标价每支8元,签字笔标价每支6元.经过沟通,这次老板给予八折优惠,那么小明最多可购买钢笔多少支?
答案:
(1)设小明原计划购买文具袋$x$个,则实际购买了$(x + 1)$个,
依题意,得$10(x + 1)×0.85 = 10x - 17$.
解得$x = 17$.
答:小明原计划购买文具袋 17 个.
(2)设小明可购买钢笔$y$支,则购买签字笔$(50 - y)$支,
依题意,得$[8y + 6(50 - y)]×80\%\leqslant400 - 10×17 + 17$.
解得$y\leqslant4.375$.
因为$y$为整数,所以$y$最大取 4.
答:小明最多可购买钢笔 4 支.
(1)设小明原计划购买文具袋$x$个,则实际购买了$(x + 1)$个,
依题意,得$10(x + 1)×0.85 = 10x - 17$.
解得$x = 17$.
答:小明原计划购买文具袋 17 个.
(2)设小明可购买钢笔$y$支,则购买签字笔$(50 - y)$支,
依题意,得$[8y + 6(50 - y)]×80\%\leqslant400 - 10×17 + 17$.
解得$y\leqslant4.375$.
因为$y$为整数,所以$y$最大取 4.
答:小明最多可购买钢笔 4 支.
1. 下列不等式总成立的是 ( )
A.$ 4 a > 2 a $
B.$ a ^ { 2 } > 0 $
C.$ a ^ { 2 } > a $
D.$ - \frac { 1 } { 2 } a ^ { 2 } \leq 0 $
A.$ 4 a > 2 a $
B.$ a ^ { 2 } > 0 $
C.$ a ^ { 2 } > a $
D.$ - \frac { 1 } { 2 } a ^ { 2 } \leq 0 $
答案:
D
2. 某不等式组的解集在数轴上表示如图7-8所示,则该不等式组可以是 ( )

A.$ \left\{ \begin{array} { l } { x - 1 < 3, } \\ { x + 1 < 3 } \end{array} \right. $
B.$ \left\{ \begin{array} { l } { x - 1 < 3, } \\ { x + 1 > 3 } \end{array} \right. $
C.$ \left\{ \begin{array} { l } { x - 1 > 3, } \\ { x + 1 > 3 } \end{array} \right. $
D.$ \left\{ \begin{array} { l } { x - 1 > 3, } \\ { x + 1 < 3 } \end{array} \right. $

A.$ \left\{ \begin{array} { l } { x - 1 < 3, } \\ { x + 1 < 3 } \end{array} \right. $
B.$ \left\{ \begin{array} { l } { x - 1 < 3, } \\ { x + 1 > 3 } \end{array} \right. $
C.$ \left\{ \begin{array} { l } { x - 1 > 3, } \\ { x + 1 > 3 } \end{array} \right. $
D.$ \left\{ \begin{array} { l } { x - 1 > 3, } \\ { x + 1 < 3 } \end{array} \right. $
答案:
B
查看更多完整答案,请扫码查看


