《2025年暑假作业本大象出版社七年级数学华师大版》

3. 如图 8 - 25,BD,CE 是$△ABC$的高,则下列结论错误的是 ( )


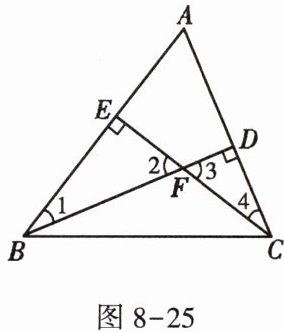
A.$∠1= ∠4$
B.$∠1+∠2+∠3+∠4= 180^{\circ }$
C.$∠BFC+∠1+∠4= 180^{\circ }$
D.$∠BFC= 180^{\circ }-∠A$

答案： C

4. 如图 8 - 26,在五边形 ABCDE 中,$AB// CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC$的外角,则$∠1+∠2+∠3$的度数为 ( )


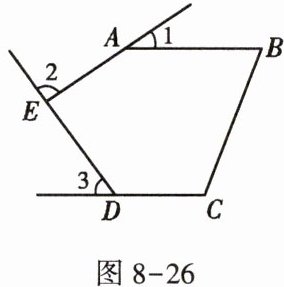
A.$90^{\circ }$
B.$180^{\circ }$
C.$120^{\circ }$
D.$270^{\circ }$

答案：
B 提示:如图,

∵ $ AB // CD $,
∴ $ ∠4 + ∠5 = 180 ^ { \circ } $.
∵ $ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360 ^ { \circ } $,
∴ $ ∠1 + ∠2 + ∠3 = 180 ^ { \circ } $.

5. 下列正多边形的组合不能铺满地面的是 ( )

A.正三角形和正五边形
B.正三角形和正方形
C.正三角形和正十二边形
D.正三角形和正六边形

答案： A

6. 有下列说法:①三角形的内角中最多有一个钝角;②三角形的中线将三角形分成面积相等的两部分;③从n边形的一个顶点可以引$(n-3)$条对角线,把n边形分成$(n-2)$个三角形,因此n边形的内角和是$(n-2)\cdot 180^{\circ }$;④六边形的对角线有3条.其中正确的有 ( )

A.4个
B.3个
C.2个
D.1个

答案： B

7. 一个正多边形的内角和为$540^{\circ }$,则这个正多边形的每一个外角的度数为____.

答案： $72 ^ { \circ }$

8. 如图 8 - 27,在四边形 ABCD 中,若去掉一个$60^{\circ }$的角得到一个五边形,则$∠1+∠2$的度数为____.

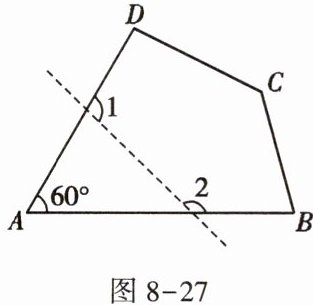
答案： $240 ^ { \circ }$

9. 如图 8 - 28,计算:$∠A+∠B+∠C+∠D+∠E+∠F$的度数为____.

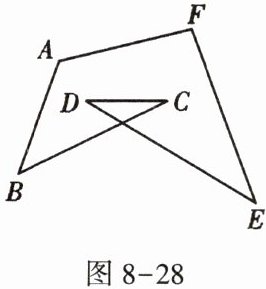
答案： $360 ^ { \circ }$

10. 一个多边形除一个内角外,其余内角之和是$2570^{\circ }$,则这个内角的度数为____.

答案： $130 ^ { \circ }$ 提示:方法一.
∵ $ 2570 ^ { \circ } ÷ 180 ^ { \circ } = 14 \cdots 50 ^ { \circ } $,
∴ 去掉的内角的度数为 $ 180 ^ { \circ } - 50 ^ { \circ } = 130 ^ { \circ } $.
方法二. 设这个内角的度数为 $ x ^ { \circ } $,边数为 $ n $,
则 $ ( n - 2 ) \cdot 180 - x = 2570 $, $ 180 \cdot n = 2930 + x $,
∴ $ n = \frac { 2930 + x } { 180 } $.
∵ $ n $ 为正整数, $ 0 ＜ x ＜ 180 $,
∴ $ n = 17 $.
∴ 这个内角的度数为 $ 180 ^ { \circ } × ( 17 - 2 ) - 2570 ^ { \circ } = 130 ^ { \circ } $.

11. 如图 8 - 29,在$△ABC$中,$∠ACB= 90^{\circ },∠A= 40^{\circ },△ABC的外角∠CBD$的平分线 BE 交 AC 的延长线于点 E.

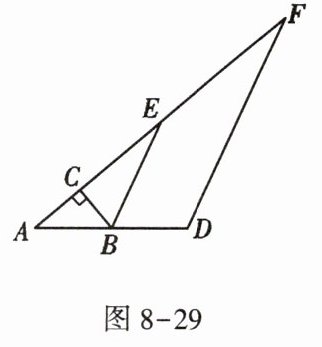
(1)求$∠CBE$的度数;
(2)过点 D 作$DF// BE$,交 AC 的延长线于点 F,求$∠F$的度数.

答案：
(1)
∵ 在 $ △ABC $ 中, $ ∠ACB = 90 ^ { \circ } $, $ ∠A = 40 ^ { \circ } $,
∴ $ ∠ABC = 90 ^ { \circ } - ∠A = 50 ^ { \circ } $.
∴ $ ∠CBD = 130 ^ { \circ } $.
∵ $ BE $ 是 $ ∠CBD $ 的平分线,
∴ $ ∠CBE = \frac { 1 } { 2 } ∠CBD = 65 ^ { \circ } $.
(2)
∵ $ ∠ACB = 90 ^ { \circ } $, $ ∠CBE = 65 ^ { \circ } $,
∴ $ ∠CEB = 90 ^ { \circ } - 65 ^ { \circ } = 25 ^ { \circ } $.
∵ $ DF // BE $,
∴ $ ∠F = ∠CEB = 25 ^ { \circ } $.