《2025年暑假作业本大象出版社七年级数学华师大版》

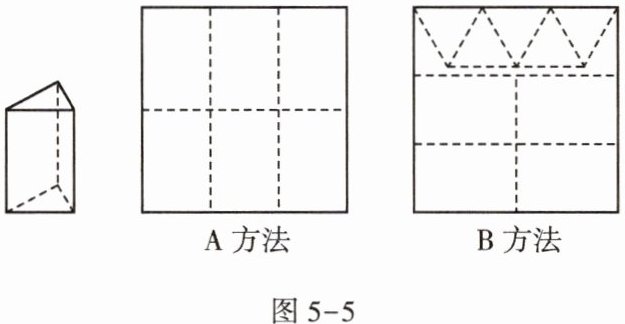
12. 用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个等边三角形底面组成,硬纸板以如图5 - 5所示的两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用含x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,能做多少个盒子?

答案：
(1)因为裁剪时$x$张用A方法，
所以裁剪时$(19 - x)$张用B方法。
所以侧面的个数为$6x + 4(19 - x) = 2x + 76$，
底面的个数为$5(19 - x) = 95 - 5x$。
(2)由题意，得$\frac{2x + 76}{3} = \frac{95 - 5x}{2}$。解得$x = 7$。
所以盒子的个数为$\frac{2×7 + 76}{3} = 30$。
答：裁剪出的侧面和底面恰好全部用完，能做30个盒子。

13. 已知A,B两地相距450km,甲、乙两车分别从A,B两地同时出发,已知甲车的平均速度为115km/h,乙车的平均速度为85km/h.
(1)两车相向而行,经过几小时两车相遇?
(2)两车相向而行,经过几小时两车相距50km?

答案：
(1)设经过$x$h两车相遇。
根据题意，得$115x + 85x = 450$。解得$x = 2.25$。
答：经过2.25h两车相遇。
(2)设经过$a$h两车相距50km。分两种情况：
①相遇前两车相距50km，
列方程为$115a + 85a = 450 - 50$。解得$a = 2$。
②相遇后两车相距50km，
列方程为$115a + 85a = 450 + 50$。解得$a = 2.5$。
答：经过2h或2.5h两车相距50km。