1. 若$m>n$,则下列不等式不一定成立的是 ( )
A.$m+3>n+3$
B.$-3m<-3n$
C.$\frac {m}{3}>\frac {n}{3}$
D.$m^{2}>n^{2}$
A.$m+3>n+3$
B.$-3m<-3n$
C.$\frac {m}{3}>\frac {n}{3}$
D.$m^{2}>n^{2}$
答案:
D
2. 不等式$x-1≤2$的非负整数解有 ( )
A.1个
B.2个
C.3个
D.4个
A.1个
B.2个
C.3个
D.4个
答案:
D
3. 不等式$3x+2<2x+3$的解集在数轴上表示正确的是图7-4中的 ( )


答案:
D
4. 不等式组$\left\{\begin{array}{l} x-3≤0,\\ \frac {1}{3}(x-2)<x+1\end{array} \right. $的解集在数轴上表示正确的是图7-5中的 ( )
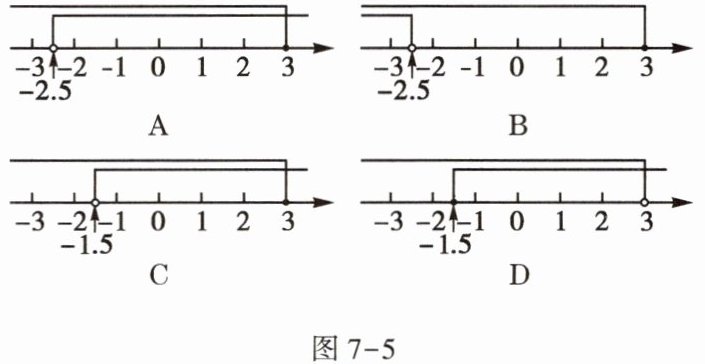

答案:
A
5. 不等式组$\left\{\begin{array}{l} 3x+1<4,\\ \frac {1}{2}(x+3)-\frac {3}{4}<0\end{array} \right. $的最大整数解是 ( )
A.0
B.-1
C.1
D.-2
A.0
B.-1
C.1
D.-2
答案:
D
6. 若关于x,y的方程组$\left\{\begin{array}{l} 2x+y= 4,\\ x+2y= -3m+2\end{array} \right. 的解满足x-y>-\frac {3}{2}$,则m可取的最小整数为 ( )
A.-3
B.-2
C.-1
D.0
A.-3
B.-2
C.-1
D.0
答案:
C 提示:$\begin{cases}2x + y = 4, & ①\\x + 2y = -3m + 2. & ②\end{cases}$
① - ②,得$x - y = 3m + 2$.
因为关于$x$,$y$的方程组$\begin{cases}2x + y = 4,\\x + 2y = -3m + 2\end{cases}$的解满足$x - y > -\frac{3}{2}$,
所以$3m + 2 > -\frac{3}{2}$. 解得$m > -\frac{7}{6}$.
所以$m$可取的最小整数为 - 1.
① - ②,得$x - y = 3m + 2$.
因为关于$x$,$y$的方程组$\begin{cases}2x + y = 4,\\x + 2y = -3m + 2\end{cases}$的解满足$x - y > -\frac{3}{2}$,
所以$3m + 2 > -\frac{3}{2}$. 解得$m > -\frac{7}{6}$.
所以$m$可取的最小整数为 - 1.
7. 不等式$\frac {1}{3}(x-m)>3-m的解集为x>1$,则m的值为____.
答案:
4
查看更多完整答案,请扫码查看


