《2025年暑假作业本大象出版社七年级数学华师大版》

1. 一个多边形的边数增加2条,则它的内角和增加 ( )

A.$ 180 ^ { \circ } $
B.$ 90 ^ { \circ } $
C.$ 360 ^ { \circ } $
D.$ 540 ^ { \circ } $

答案： C

2. 下列长度的三条线段能组成三角形的是 ( )

A.$ 2 \mathrm { cm }, 3 \mathrm { cm }, 4 \mathrm { cm } $
B.$ 2 \mathrm { cm }, 3 \mathrm { cm }, 5 \mathrm { cm } $
C.$ 3 \mathrm { cm }, 5 \mathrm { cm }, 9 \mathrm { cm } $
D.$ 8 \mathrm { cm }, 4 \mathrm { cm }, 4 \mathrm { cm } $

答案： A

3. 已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为 ( )

A.7
B.8
C.9
D.10

答案： C

4. 小明把一副含$ 45 ^ { \circ }, 30 ^ { \circ } $的直角三角板按如图8-16摆放,其中$ \angle C = \angle F = 90 ^ { \circ } $,$ \angle A = 45 ^ { \circ }, \angle D = 30 ^ { \circ } $,则$ \angle \alpha + \angle \beta $等于( )


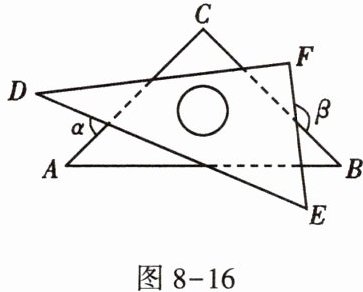
A.$ 180 ^ { \circ } $
B.$ 210 ^ { \circ } $
C.$ 360 ^ { \circ } $
D.$ 270 ^ { \circ } $

答案： B

5. 如图8-17,在五边形$ A B C D E $中,$ \angle A + \angle B + \angle E = 300 ^ { \circ }, D P, C P 分别平分 \angle E D C, \angle B C D $,则$ \angle P $的度数是 ( )


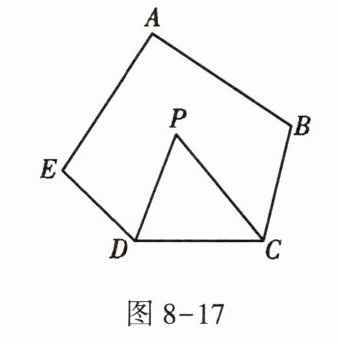
A.$ 50 ^ { \circ } $
B.$ 55 ^ { \circ } $
C.$ 60 ^ { \circ } $
D.$ 65 ^ { \circ } $

答案： C 提示:
∵ 在五边形 ABCDE 中,$∠A+∠B+∠E=300^{\circ },$
$\therefore ∠EDC+∠BCD=240^{\circ }.$
又
∵ DP,CP 分别平分$∠EDC,∠BCD,$
$\therefore ∠PDC+∠PCD=120^{\circ }.$
$\therefore$ 在$\triangle CDP$中,$∠P=180^{\circ }-(∠PDC+∠PCD)=180^{\circ }-120^{\circ }=60^{\circ }.$

6. 如图8-18,$ D, E 是 \triangle A B C 的边 A B $,$ A C $上一点,把$ \triangle A B C 沿 D E $折叠,当点$ A 落在四边形 B C E D 内部的点 A ^ { \prime } $时,则$ \angle A 与 \angle 1 + \angle 2 $之间的数量关系是 ( )


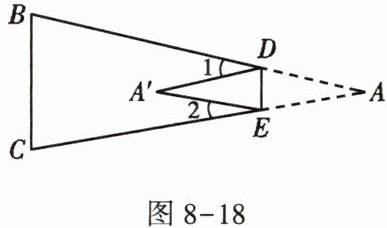
A.$ 2 \angle A = \angle 1 + \angle 2 $
B.$ \angle A = \angle 1 + \angle 2 $
C.$ 3 \angle A = 2 \angle 1 + \angle 2 $
D.$ 3 \angle A = 2 ( \angle 1 + \angle 2 ) $

答案：
A 提示:如图,
∵ 折叠后 A 和$A'$重合,

$\therefore ∠A'DE=∠ADE,∠AED=∠A'ED.$
$\because ∠ADE+∠AED=180^{\circ }-∠A,$
$\therefore ∠1+∠2=360^{\circ }-2(∠ADE+∠AED)=360^{\circ }-2(180^{\circ }-∠A)=2∠A.$

7. 若一个多边形的内角和与外角和之和是$ 900 ^ { \circ } $,则该多边形的边数是______.

答案： 5

8. 将两张三角形纸片如图8-19摆放,量得$ \angle 1 + \angle 2 + \angle 3 + \angle 4 = 220 ^ { \circ } $,则$ \angle 5 $的度数为______.

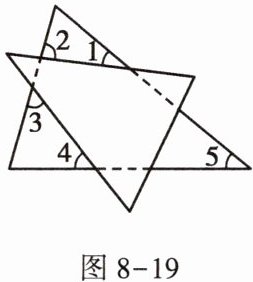
答案： $40^{\circ }$