《2025年暑假作业本大象出版社七年级数学华师大版》

3. 已知$\triangle ABC的一个外角为50^{\circ}$,则$\triangle ABC$一定是( )

A.锐角三角形
B.钝角三角形
C.直角三角形
D.锐角三角形或钝角三角形

答案： B

4. 若$\triangle ABC三边的长度分别为m$,$n$,$p$,且$\vert m - n\vert+(n - p)^{2}= 0$,则这个三角形为( )

A.钝角三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形

答案： B

5. 现有若干个三角形,在所有的内角中,有$5$个直角,$3$个钝角,$25$个锐角,则在这些三角形中锐角三角形的个数是( )

A.$3$
B.$4或5$
C.$6或7$
D.$8$

答案： A

1. 下列说法正确的是( )

A.三角形的角平分线是射线
B.过三角形的顶点,且过对边中点的直线是三角形的一条中线
C.一个锐角三角形同一边上的中线、高及这条边所对的角的平分线中,高最短
D.三角形的高、中线、角平分线一定在三角形的内部

答案： C

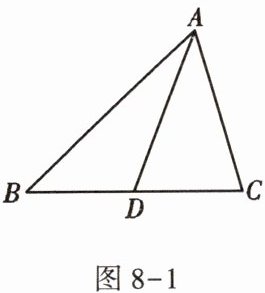
2. 如图$8 - 1$,$AD是\triangle ABC$的中线,已知$\triangle ABD比\triangle ACD的周长大6cm$,则$AB与AC$的差为( )


A.$2cm$
B.$3cm$
C.$6cm$
D.$12cm$

答案： C

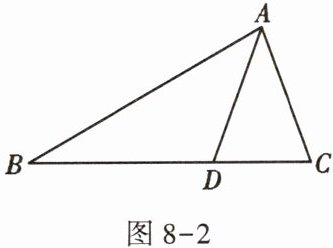
3. 如图$8 - 2$,在$\triangle ABC$中,$AD平分\angle BAC交BC于点D$,$\angle B = 30^{\circ}$,$\angle ADC = 70^{\circ}$,则$\angle C$的度数是( )


A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$

答案： C

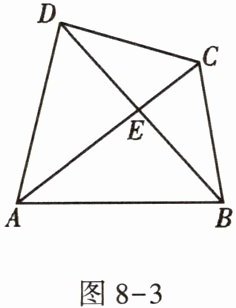
4. 如图$8 - 3$,四边形$ABCD的对角线AC和BD相交于点E$,如果$\triangle CDE的面积为3$,$\triangle BCE的面积为4$,$\triangle ADE的面积为6$,那么$\triangle ABE$的面积为( )


A.$7$
B.$8$
C.$9$
D.$10$

答案： B　提示:
∵ $ S_{△CDE} = 3 $，$ S_{△ADE} = 6 $，
∴ $ CE:AE = 3:6 = 1:2 $（高相等，面积比等于底的比）。
∴ $ S_{△BCE}:S_{△ABE} = CE:AE = 1:2 $。
又
∵ $ S_{△BCE} = 4 $，
∴ $ S_{△ABE} = 8 $。

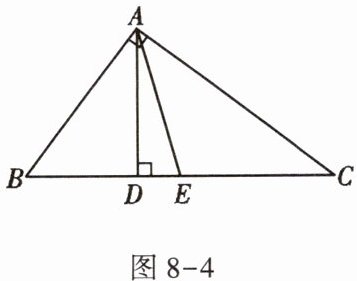
5. 如图$8 - 4$,已知$AD$,$AE分别是\triangle ABC$的高和中线,$AB = 6cm$,$AC = 8cm$,$BC = 10cm$,$\angle CAB = 90^{\circ}$. 试求：
(1)$AD$的长度；
(2)$\triangle ABE$的面积；
(3)$\triangle ACE和\triangle ABE$的周长的差.

答案：
(1)
∵ $ ∠BAC = 90° $，AD 是边 BC 上的高，
∴ $ \frac{1}{2}AB·AC = \frac{1}{2}BC·AD $。
∴ $ AD = \frac{AB·AC}{BC} = \frac{6×8}{10} = 4.8(cm) $，
即 AD 的长度为 4.8cm。
(2)
∵ $ △ABC $ 是直角三角形，$ ∠BAC = 90° $，$ AB = 6cm $，$ AC = 8cm $，
∴ $ S_{△ABC} = \frac{1}{2}AB·AC = \frac{1}{2}×6×8 = 24(cm²) $。
又
∵ AE 为 BC 边上的中线，
∴ $ BE = EC $。
∴ $ \frac{1}{2}BE·AD = \frac{1}{2}EC·AD $，即 $ S_{△ABE} = S_{△AEC} $。
∴ $ S_{△ABE} = \frac{1}{2}S_{△ABC} = 12 cm² $。
∴ $ △ABE $ 的面积是 $ 12 cm² $。
(3)
∵ AE 为 BC 边上的中线，
∴ $ BE = CE $。
∴ $ △ACE $ 的周长 - $ △ABE $ 的周长 $ = AC + AE + CE - (AB + BE + AE) = AC - AB = 8 - 6 = 2(cm) $，
即 $ △ACE $ 和 $ △ABE $ 的周长的差是 2 cm。