13. 我们知道,在三角形每一顶点处各取一个外角,它们的和就是这个三角形的外角和.
(1)你能求出三角形的外角和是多少吗? 证明你的结论.
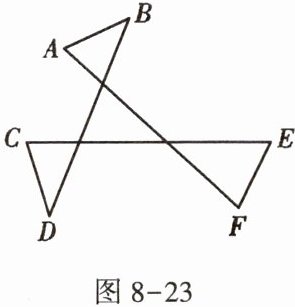
(2)如果将三角形三条边都向两边延长,并且在每条线上任取两点连接起来,那么在原三角形外又得到三个新三角形,如图8-23,猜想$ \angle A, \angle B, \angle C, \angle D, \angle E, \angle F $的和是多少.
(3)请用(1)的结论说明(2)的猜想.
(4)对于(2),你有其他的方法吗? 请写出来与同伴交流.
(1)你能求出三角形的外角和是多少吗? 证明你的结论.
(2)如果将三角形三条边都向两边延长,并且在每条线上任取两点连接起来,那么在原三角形外又得到三个新三角形,如图8-23,猜想$ \angle A, \angle B, \angle C, \angle D, \angle E, \angle F $的和是多少.
(3)请用(1)的结论说明(2)的猜想.
(4)对于(2),你有其他的方法吗? 请写出来与同伴交流.

答案:
(1)三角形的外角和等于$360^{\circ }$.如图①所示,
$\because ∠1$是$\triangle ABC$的外角,

$\therefore ∠1=∠ABC+∠ACB.$
同理,得$∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC.$
$\therefore ∠1+∠2+∠3=(∠ABC+∠ACB)+(∠ABC+∠BAC)+(∠ACB+∠BAC)=2(∠ABC+∠ACB+∠BAC).$
$\because ∠ABC+∠ACB+∠BAC=180^{\circ },$
$\therefore ∠1+∠2+∠3=360^{\circ }.$
(2)猜想:$∠A+∠B+∠C+∠D+∠E+∠F=360^{\circ }.$
(3)证明:如图②所示,
$\because ∠AGM$是$\triangle ABG$的外角,
$\therefore ∠AGM=∠A+∠B.$
$\because ∠MNF$是$\triangle EFN$的外角,
$\therefore ∠MNF=∠E+∠F.$
$\because ∠DMN$是$\triangle CDM$的外角,
$\therefore ∠DMN=∠C+∠D.$
$\because ∠AGM,∠MNF,∠DMN$是$\triangle GMN$的外角,
$\therefore ∠AGM+∠MNF+∠DMN=360^{\circ },$
即$∠A+∠B+∠C+∠D+∠E+∠F=360^{\circ }.$

(4)如图③所示,$\because ∠2+∠4+∠5=180^{\circ },$
$\therefore ∠1+∠3+∠6=180^{\circ }.$
$\because ∠A+∠B+∠1=180^{\circ },∠C+∠D+∠3=180^{\circ },∠E+∠F+∠6=180^{\circ },$
$\therefore ∠A+∠B+∠C+∠D+∠E+∠F+∠1+∠3+∠6=180^{\circ }×3=540^{\circ }.$
$\therefore ∠A+∠B+∠C+∠D+∠E+∠F=360^{\circ }.$
(1)三角形的外角和等于$360^{\circ }$.如图①所示,
$\because ∠1$是$\triangle ABC$的外角,

$\therefore ∠1=∠ABC+∠ACB.$
同理,得$∠2=∠ABC+∠BAC,∠3=∠ACB+∠BAC.$
$\therefore ∠1+∠2+∠3=(∠ABC+∠ACB)+(∠ABC+∠BAC)+(∠ACB+∠BAC)=2(∠ABC+∠ACB+∠BAC).$
$\because ∠ABC+∠ACB+∠BAC=180^{\circ },$
$\therefore ∠1+∠2+∠3=360^{\circ }.$
(2)猜想:$∠A+∠B+∠C+∠D+∠E+∠F=360^{\circ }.$
(3)证明:如图②所示,
$\because ∠AGM$是$\triangle ABG$的外角,
$\therefore ∠AGM=∠A+∠B.$
$\because ∠MNF$是$\triangle EFN$的外角,
$\therefore ∠MNF=∠E+∠F.$
$\because ∠DMN$是$\triangle CDM$的外角,
$\therefore ∠DMN=∠C+∠D.$
$\because ∠AGM,∠MNF,∠DMN$是$\triangle GMN$的外角,
$\therefore ∠AGM+∠MNF+∠DMN=360^{\circ },$
即$∠A+∠B+∠C+∠D+∠E+∠F=360^{\circ }.$

(4)如图③所示,$\because ∠2+∠4+∠5=180^{\circ },$
$\therefore ∠1+∠3+∠6=180^{\circ }.$
$\because ∠A+∠B+∠1=180^{\circ },∠C+∠D+∠3=180^{\circ },∠E+∠F+∠6=180^{\circ },$
$\therefore ∠A+∠B+∠C+∠D+∠E+∠F+∠1+∠3+∠6=180^{\circ }×3=540^{\circ }.$
$\therefore ∠A+∠B+∠C+∠D+∠E+∠F=360^{\circ }.$
1. 若一个三角形三个内角的度数之比为$1:2:3$,则这个三角形是 ( )
A.锐角三角形
B.等边三角形
C.钝角三角形
D.直角三角形
A.锐角三角形
B.等边三角形
C.钝角三角形
D.直角三角形
答案:
D
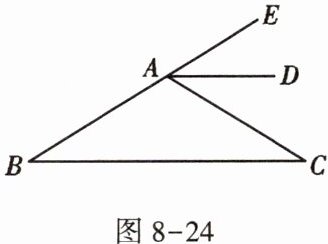
2. 如图 8 - 24,AD 是$△ABC的外角∠EAC$的平分线,$AD// BC,∠B= 32^{\circ }$,则$∠C$的度数是 ( )
A.$64^{\circ }$
B.$32^{\circ }$
C.$30^{\circ }$
D.$40^{\circ }$

A.$64^{\circ }$
B.$32^{\circ }$
C.$30^{\circ }$
D.$40^{\circ }$
答案:
B
查看更多完整答案,请扫码查看


