9. 用一条宽度相等的足够长的纸条打一个结(如图8-20①所示),然后轻轻拉紧、压平就可以得到如图8-20②所示的正五边形$ A B C D E $,则图8-20②中$ \angle B A C $的度数为______.
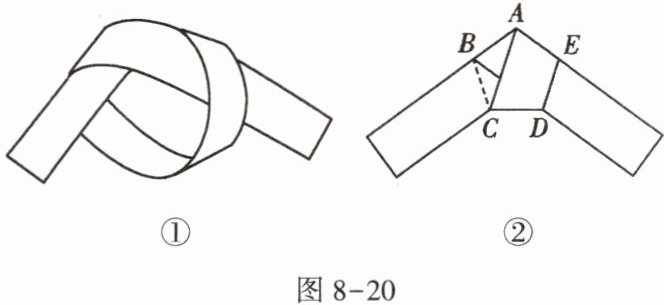

答案:
$36^{\circ }$
10. 已知$ a, b, c 是 \triangle A B C $的三边长,且$ a, b 满足 | a - 7 | + ( b - 1 ) ^ { 2 } = 0, c $为奇数,则$ c = $______.
答案:
7
11. 如图8-21,已知$ D 是 \triangle A B C 的边 B C $延长线上一点,$ D F \perp A B 交 A B 于点 F $,交$ A C 于点 E, \angle A = 46 ^ { \circ }, \angle D = 50 ^ { \circ } $.求$ \angle A C B $的度数.
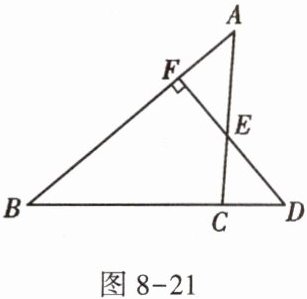

答案:
在$\triangle DFB$中,
$\because DF⊥AB,\therefore ∠DFB=90^{\circ }.$
又$\because ∠D=50^{\circ },∠DFB+∠D+∠B=180^{\circ },$
$\therefore ∠B=40^{\circ }.$
在$\triangle ABC$中,$∠A=46^{\circ },∠B=40^{\circ },$
$\therefore ∠ACB=180^{\circ }-∠A-∠B=94^{\circ }.$
$\therefore ∠ACB$的度数是$94^{\circ }.$
$\because DF⊥AB,\therefore ∠DFB=90^{\circ }.$
又$\because ∠D=50^{\circ },∠DFB+∠D+∠B=180^{\circ },$
$\therefore ∠B=40^{\circ }.$
在$\triangle ABC$中,$∠A=46^{\circ },∠B=40^{\circ },$
$\therefore ∠ACB=180^{\circ }-∠A-∠B=94^{\circ }.$
$\therefore ∠ACB$的度数是$94^{\circ }.$
12. 探索题:任意三角形的内角和为$ 180 ^ { \circ } $,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.

根据图8-22所示,填空:
(1)一个四边形可以分成______个三角形,于是四边形的内角和为______;
(2)一个五边形可以分成______个三角形,于是五边形的内角和为______;
(3)按此规律,$ n $边形可以分成______个三角形,于是$ n $边形的内角和为______.

根据图8-22所示,填空:
(1)一个四边形可以分成______个三角形,于是四边形的内角和为______;
(2)一个五边形可以分成______个三角形,于是五边形的内角和为______;
(3)按此规律,$ n $边形可以分成______个三角形,于是$ n $边形的内角和为______.
答案:
(1)2 $360^{\circ }$
(2)3 $540^{\circ }$
(3)$(n-2)$ $(n-2)\cdot 180^{\circ }$
(1)2 $360^{\circ }$
(2)3 $540^{\circ }$
(3)$(n-2)$ $(n-2)\cdot 180^{\circ }$
查看更多完整答案,请扫码查看


