《2025年暑假作业本大象出版社七年级数学华师大版》

1. 正九边形的一个内角的度数是( )

A.$108^{\circ}$
B.$120^{\circ}$
C.$135^{\circ}$
D.$140^{\circ}$

答案： D

2. 图$8 - 9为长方形ABCD$,一条直线将该长方形分割成两个多边形,若这两个多边形的内角和分别为$a和b$,则$a + b$不可能是( )


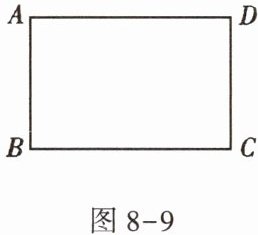
A.$360^{\circ}$
B.$540^{\circ}$
C.$630^{\circ}$
D.$720^{\circ}$

答案： C

3. 如图$8 - 10$,小华从点$A$出发,沿直线前进$10m后左转24^{\circ}$,再沿直线前进$10m$,又向左转$24^……{\circ}$照这样走下去,他第一次回到出发地点$A$时,一共走的路程是( )


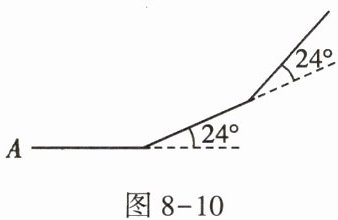
A.$140m$
B.$150m$
C.$160m$
D.$240m$

答案： B

4. 如图$8 - 11$,在四边形$ABCD$中,$\angle A+\angle D= \alpha$,$\angle ABC的平分线与\angle BCD的平分线交于点P$,则$\angle P$的度数为( )


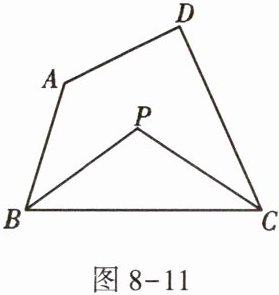
A.$90^{\circ}-\frac{1}{2}\alpha$
B.$90^{\circ}+\frac{1}{2}\alpha$
C.$\frac{1}{2}\alpha$
D.$360^{\circ}-\alpha$

答案： C　提示:
∵ 在四边形 ABCD 中，
∴ $ ∠ABC + ∠BCD = 360° - (∠A + ∠D) = 360° - α $。
∵ BP，CP 分别为 $ ∠ABC $，$ ∠BCD $ 的平分线，
∴ $ ∠PBC + ∠PCB = \frac{1}{2}(∠ABC + ∠BCD) = \frac{1}{2}(360° - α) = 180° - \frac{1}{2}α $。
∴ $ ∠P = 180° - (∠PBC + ∠PCB) = 180° - (180° - \frac{1}{2}α) = \frac{1}{2}α $。

5. 如图$8 - 12$,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为$2340^{\circ}$的新多边形,则原多边形的边数为( )


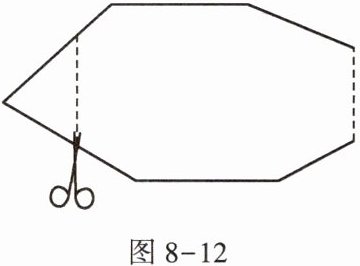
A.$13$
B.$14$
C.$15$
D.$16$

答案： B

6. 如图$8 - 13$,在六边形$ABCDEF$中,$AF// CD$,$AB// DE$,且$\angle BAF = 100^{\circ}$,$\angle BCD = 120^{\circ}$,求$\angle CDE和\angle ABC$的度数.

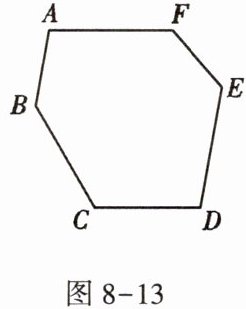
答案：
如图，连接 AD。
∵ $ AF // CD $，$ AB // DE $，
　　　　　　
∴ $ ∠FAD = ∠ADC $，$ ∠BAD = ∠ADE $。
∴ $ ∠CDE = ∠BAF = 100° $。
∵ 在四边形 ABCD 中，
∴ $ ∠ABC + ∠DCB + ∠BAD + ∠ADC = 360° $。
又
∵ $ ∠FAB = ∠FAD + ∠BAD = ∠ADC + ∠BAD = 100° $，
∴ $ ∠ABC = 360° - 120° - 100° = 140° $。