第132页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
7. 下列四边形:①平行四边形;②矩形;③菱形;④正方形。其中四个顶点都在同一个圆上的有
②④
。(填序号)
答案:
②④
8. 如图,OA,OB为⊙O的半径,C,D分别是OA,OB的中点,连接AD,BC交于点E。求证:
(1)∠A=∠B;
证明:因为OA,OB为⊙O的半径,所以OA=OB。
又因为C,D分别是OA,OB的中点,所以OC=
在△ODA和△OCB中,
所以∠A=∠B。
(2)AE=BE。
证明:连接AB。
因为OA=OB,所以∠OAB=∠OBA(
又因为已证∠A=∠B,即∠OAD=∠OBC,所以∠OAB-∠OAD=∠OBA-∠OBC,即∠EAB=∠EBA。
根据
(1)∠A=∠B;
证明:因为OA,OB为⊙O的半径,所以OA=OB。
又因为C,D分别是OA,OB的中点,所以OC=
1/2OA
,OD=1/2OB
,则OC=OD。在△ODA和△OCB中,
{OA=OB,∠AOD=∠BOC,OD=OC}
(对顶角相等),根据SAS
定理可得△ODA≌△OCB。所以∠A=∠B。
(2)AE=BE。
证明:连接AB。
因为OA=OB,所以∠OAB=∠OBA(
等边对等角
)。又因为已证∠A=∠B,即∠OAD=∠OBC,所以∠OAB-∠OAD=∠OBA-∠OBC,即∠EAB=∠EBA。
根据
等角对等边
,可得AE=BE。
答案:
【解析】:
(1) 因为 $OA$,$OB$ 为$\odot O$的半径,所以 $OA = OB$。
又因为 $C$,$D$ 分别是 $OA$,$OB$ 的中点,所以 $OC=\frac{1}{2}OA$,$OD=\frac{1}{2}OB$,则 $OC = OD$。
在$\triangle ODA$和$\triangle OCB$中,$\left\{\begin{array}{l}OA = OB\\\angle AOD=\angle BOC\\OD = OC\end{array}\right.$(对顶角相等),根据 $SAS$(边角边)定理可得$\triangle ODA\cong\triangle OCB$。
所以$\angle A=\angle B$。
(2) 连接 $AB$。
因为 $OA = OB$,所以$\angle OAB=\angle OBA$(等边对等角)。
又因为已证$\angle A=\angle B$,即$\angle OAD=\angle OBC$,所以$\angle OAB-\angle OAD=\angle OBA - \angle OBC$,即$\angle EAB=\angle EBA$。
根据等角对等边,可得 $AE = BE$。
【答案】:
(1) $\angle A=\angle B$得证。
(2) $AE = BE$得证。
(1) 因为 $OA$,$OB$ 为$\odot O$的半径,所以 $OA = OB$。
又因为 $C$,$D$ 分别是 $OA$,$OB$ 的中点,所以 $OC=\frac{1}{2}OA$,$OD=\frac{1}{2}OB$,则 $OC = OD$。
在$\triangle ODA$和$\triangle OCB$中,$\left\{\begin{array}{l}OA = OB\\\angle AOD=\angle BOC\\OD = OC\end{array}\right.$(对顶角相等),根据 $SAS$(边角边)定理可得$\triangle ODA\cong\triangle OCB$。
所以$\angle A=\angle B$。
(2) 连接 $AB$。
因为 $OA = OB$,所以$\angle OAB=\angle OBA$(等边对等角)。
又因为已证$\angle A=\angle B$,即$\angle OAD=\angle OBC$,所以$\angle OAB-\angle OAD=\angle OBA - \angle OBC$,即$\angle EAB=\angle EBA$。
根据等角对等边,可得 $AE = BE$。
【答案】:
(1) $\angle A=\angle B$得证。
(2) $AE = BE$得证。
9. 如图,点A,D,G,M在以点O为圆心的半圆上,四边形ABOC,DEOF,HMNO均为矩形。设BC=a,EF=b,NH=c,则下列各式中正确的是 (
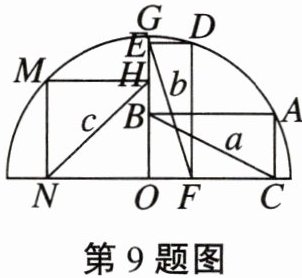
A. a>b>c
B. b>c>a
C. c>a>b
D. a=b=c
D
)
A. a>b>c
B. b>c>a
C. c>a>b
D. a=b=c
答案:
D
10. 如图,在Rt△ABC中,∠C=90°,AB=10。若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AC的长为

$5\sqrt{3}$
。
答案:
$5\sqrt{3}$
11. 【问题情境】筒车是我国古代发明的一种水利灌溉工具,既经济又环保,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①)。假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒。
【问题设置】把筒车抽象为一个半径为r的⊙O。如图②,OM始终垂直于水平面,设筒车半径为2米。当t=0时,某盛水筒恰好位于水面点A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处。(参考数据,√2≈1.414,√3≈1.732)
【问题解决】
(1)求该盛水筒从点A处逆时针旋转到点B处时,∠BOM的度数;
(2)求该盛水筒旋转至点B处时,它到水面的距离。(结果精确到0.1米)
【问题设置】把筒车抽象为一个半径为r的⊙O。如图②,OM始终垂直于水平面,设筒车半径为2米。当t=0时,某盛水筒恰好位于水面点A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处。(参考数据,√2≈1.414,√3≈1.732)
【问题解决】
(1)求该盛水筒从点A处逆时针旋转到点B处时,∠BOM的度数;
45°
(2)求该盛水筒旋转至点B处时,它到水面的距离。(结果精确到0.1米)
0.3 米
答案:
(1)$∠BOM = 45^{\circ}$.
(2)0.3 米.
(1)$∠BOM = 45^{\circ}$.
(2)0.3 米.
查看更多完整答案,请扫码查看


