《2025年启航新课堂九年级数学上册人教版》

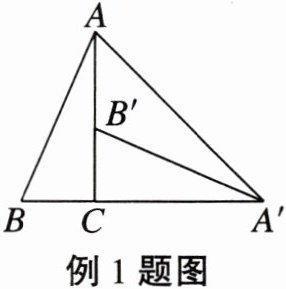
例1 如图，在$\triangle ABC$中，$\angle ACB=90^{\circ}$，$\angle BAC=\alpha$。将$\triangle ABC$绕点$C$顺时针旋转$90^{\circ}$得到$\triangle A^{\prime}B^{\prime}C$，点$B$的对应点$B^{\prime}$在边$AC$上（不与点$A$，$C$重合），则$\angle AA^{\prime}B^{\prime}$的度数为（C）

A. $\alpha$
B. $\alpha - 45^{\circ}$
C. $45^{\circ}-\alpha$
D. $90^{\circ}-\alpha$

答案： C

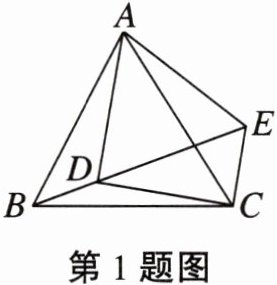
1. 如图，在等边$\triangle ABC$中，$D$为$\triangle ABC$内的一点，$\angle ADB=120^{\circ}$，$\angle ADC=90^{\circ}$，将$\triangle ABD$绕点$A$逆时针旋转得到$\triangle ACE$，则$\angle DCE$的度数为$90^{\circ}$。

答案： $ 90 ^ { \circ } $

2. 如图，在正方形$ABCD$内有一点$P$，$PA=1$，$PD=2$，$PC=3$，则$\angle APD$的度数为$135^{\circ}$。

答案： $ 135 ^ { \circ } $

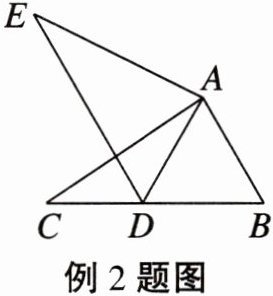
例2 如图，在$\triangle ABC$中，$AB=2$，$BC=3.6$，$\angle B=60^{\circ}$。将$\triangle ABC$绕点$A$顺时针旋转得到$\triangle ADE$，当点$B$的对应点$D$恰好落在$BC$边上时，$CD$的长为（A）

A. $1.6$
B. $1.8$
C. $2$
D. $2.6$

答案： A

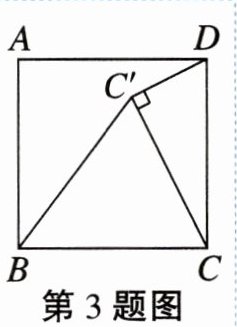
3. 如图，在正方形$ABCD$中，将边$BC$绕点$B$逆时针旋转得到$BC^{\prime}$。若$\angle CC^{\prime}D=90^{\circ}$，$C^{\prime}D=2$，则线段$BC^{\prime}$的长为（D）

A. $4$
B. $2\sqrt{3}$
C. $6$
D. $2\sqrt{5}$

答案： D

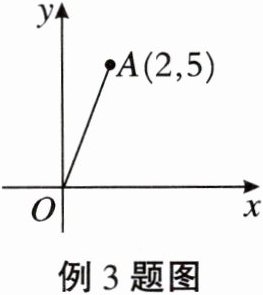
例3 如图，在平面直角坐标系中，点$A$的坐标为$(2,5)$。将线段$OA$绕原点$O$逆时针旋转$90^{\circ}$，得到线段$OA^{\prime}$，则点$A^{\prime}$的坐标为（A）

A. $(-5,2)$
B. $(5,2)$
C. $(2,-5)$
D. $(5,-2)$

答案： A

4. 如图，在平面直角坐标系中，将边长为$2$个单位长度的正方形$ABCO$绕原点$O$逆时针旋转$75^{\circ}$，再沿$y$轴向上平移$1$个单位长度，则点$B^{\prime\prime}$的坐标为$ ( - \sqrt { 2 } , \sqrt { 6 } + 1 ) $。

答案： $ ( - \sqrt { 2 } , \sqrt { 6 } + 1 ) $

5. （2024达州模拟）如图，在平面直角坐标系中，点$A$，$B$的坐标分别为$(1,0)$，$(1,\sqrt{3})$，将$\triangle OAB$绕原点$O$顺时针旋转$60^{\circ}$，再将其各边都扩大为原来的$2$倍，使得$OA_{1}=2OA$，$OB_{1}=2OB$，得到$\triangle OA_{1}B_{1}$；将$\triangle OA_{1}B_{1}$绕原点$O$顺时针旋转$60^{\circ}$，再将其各边都扩大为原来的$2$倍，使得$OA_{2}=2OA_{1}$，$OB_{2}=2OB_{1}$，得到$\triangle OA_{2}B_{2}$；$\cdots$，如此继续下去，得到$\triangle OA_{2023}B_{2023}$，则点$A_{2023}$的坐标是$ ( 2 ^ { 2022 } , - \sqrt { 3 } × 2 ^ { 2022 } ) $。

答案： $ ( 2 ^ { 2022 } , - \sqrt { 3 } × 2 ^ { 2022 } ) $