第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
可以把圆放在方格纸中利用数方格的形式估算圆的面积。圆的面积能不能像正方形、长方形、平行四边形等利用公式进行计算呢?
例 怎样推导圆的面积计算公式?
分析:把圆转化成我们学过的图形。
(1)平面图形的大小叫作它们的面积。同样,一个圆的面积就是这个圆所占平面的大小。
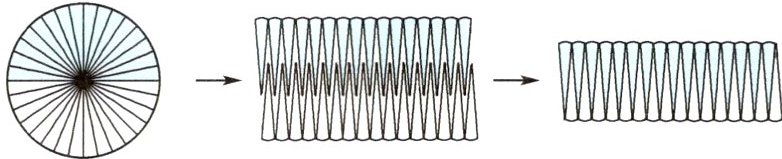
(2)尝试把圆转化为平行四边形。如下图,把一个圆平均分成若干份,可以拼成一个近似的平行四边形,这个近似的平行四边形的面积与圆的面积相等。平行四边形的底等于( ),高等于( )。

(3)公式推导。

方法总结
如果用S表示圆的面积,r表示圆的半径,那么圆的面积计算公式为S=( )。
例 怎样推导圆的面积计算公式?
分析:把圆转化成我们学过的图形。
(1)平面图形的大小叫作它们的面积。同样,一个圆的面积就是这个圆所占平面的大小。
(2)尝试把圆转化为平行四边形。如下图,把一个圆平均分成若干份,可以拼成一个近似的平行四边形,这个近似的平行四边形的面积与圆的面积相等。平行四边形的底等于( ),高等于( )。

(3)公式推导。

方法总结
如果用S表示圆的面积,r表示圆的半径,那么圆的面积计算公式为S=( )。
答案:
圆周长的一半 圆的半径 $\pi r^{2}$
@@圆周长的一半 圆的半径 $\pi r^{2}$
@@圆周长的一半 圆的半径 $\pi r^{2}$
(迁移探究)如图,把一个圆平均分成若干份,可以剪拼成一个近似的长方形。剪拼成的长方形的面积与圆的面积相等。长方形的长等于( ),宽等于( )。因为长方形的面积=( )×( ),所以圆的面积=( )×( )=( )×( )=( )。(最后三个空填字母或含有字母的式子)

答案:
圆周长的一半 圆的半径 长 宽 圆周长的一半 圆的半径 $\pi r$ $r$ $\pi r^{2}$
1. 把一个半径是8cm的圆平均分成若干份,剪开后拼成一个近似的长方形。这个长方形的长是( )cm,宽是( )cm,面积是( )cm²,因此圆的面积是( )cm²。
答案:
25.12 8 200.96 200.96
查看更多完整答案,请扫码查看


