《2025年阳光同学暑假衔接五升六年级数学北师大版》

例1将图中的长方体切成两个小长方体,表面积可能增加多少平方厘米?

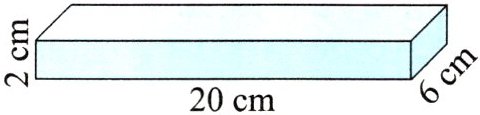
思路点拨 把一个长方体切成两个小长方体会增加2个面,从不同的方向切长方体,其表面积增加的大小可能不同。所以解决此类问题可以分情况:垂直长切,表面积增加多少;垂直宽切,表面积增加多少;垂直高切,表面积增加多少。
尝试解答

答案： 第1种:垂直长切，表面积增加:
$2×6×2=24(cm^{2})$
第2种:垂直宽切，表面积增加:
$2×20×2=80(cm^{2})$
第3种:垂直高切，表面积增加:
$20×6×2=240(cm^{2})$
表面积可能增加$24cm^{2}$、$80cm^{2}$或$240cm^{2}$

1.(仿例练习)将图中的长方体切成棱长为7cm的正方体,切完后两个正方体的表面积之和比原长方体的表面积多多少平方厘米?

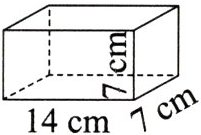
答案： $7×7×2=98(cm^{2})$

2.(变式提升)把两个长7cm、宽5cm、高3cm的长方体拼成一个大长方体,拼成的大长方体的表面积最大是多少平方厘米? 最小是多少平方厘米?

答案：
将最小的面合在一起表面积最大，如图:
新拼成的长方体长$7×2=14(cm)$，宽5cm，高3cm
$(14×5+14×3+5×3)×2=254(cm^{2})$
将最大的面合在一起表面积最小，如图:

新拼成的长方体长7cm，宽5cm，高$3×2=6(cm)$
$(7×5+7×6+5×6)×2=214(cm^{2})$

3.(素养培优)把两个长18cm、宽12cm、高2cm的长方体礼盒用纸打包到一起,怎样摆放两个礼盒最省包装纸? 最少需要多少包装纸? (忽略折叠的包装纸损耗)

答案：
将最大的面合在一起最省包装纸，
如图:

新拼成的长方体长18cm，宽12cm，高$2×2=4(cm)$
$(18×12+18×4+12×4)×2=672(cm^{2})$