2025年小考金卷王六年级数学全一册通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小考金卷王六年级数学全一册通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
3. 一件工作,甲单独做需10小时完成,乙单独做需12小时完成,丙单独做需15小时完成。现在三人合作,但甲因中途另有任务提前撤出,结果这项工作用了6小时完成,甲在其中做了多少小时?(5分)
答案:
$[1 - (\frac{1}{12}+\frac{1}{15})×6]÷\frac{1}{10}=1$(小时) 答:甲做了 1 小时。
4. 有两盒棋子,第一盒中棋子枚数是第二盒的$\frac{3}{5}$,如果从第一盒中取出20枚棋子放入第二盒,则第一盒的枚数是第二盒的$\frac{1}{3}$。原来第一盒有多少枚棋子?(5分)
答案:
解:设第二盒原来有$x$枚棋子。 $\frac{3}{5}x - 20=(x + 20)×\frac{1}{3}$ $x = 100$ 当$x = 100$时,$\frac{3}{5}x=\frac{3}{5}×100 = 60$ 答:原来第一盒有 60 枚棋子。
5. 商店以每本4.5元的价格进了一批纪念册,开始出售时营业员把单价搞错了,按每本4元零售价卖出了全部的$\frac{3}{8}$,接着把剩下的以每本6元卖出,当全部卖出时,还能获利630元。这批纪念册共有多少本?(5分)
答案:
解:设这批纪念册有$x$本。 $\frac{3}{8}x×4+(1 - \frac{3}{8})x×6 - 4.5x = 630$ $x = 840$ 答:这批纪念册共有 840 本。
6. 有一个长方体容器,里面装有水,测得水面高度为4.4 cm(如图1),为了得到冰水(冰水可用于水果保鲜),妈妈把一根圆柱形的冰柱垂直放入其中,水面升高至5.5 cm,这时刚好有$\frac{1}{3}$冰柱浸没在水中(如图2)。(7分)
(1)求冰柱的体积。(3分)
(2)求该冰柱完全融化时容器内的水面高度。(已知:冰融化成水后体积会减少原来的$\frac{1}{11}$)(4分)

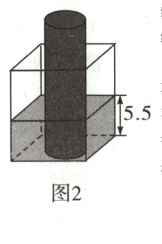
(1)求冰柱的体积。(3分)
(2)求该冰柱完全融化时容器内的水面高度。(已知:冰融化成水后体积会减少原来的$\frac{1}{11}$)(4分)


答案:
(1)$10×10×(5.5 - 4.4)÷\frac{1}{3}=330(cm^{3})$ 答:冰柱的体积为$330 cm^{3}$。
答:冰柱的体积为$330 cm^{3}$。
(2)冰融化成水的体积为$330×(1 - \frac{1}{11})=300(cm^{3})$ $300÷(10×10)+4.4 = 7.4(cm)$ 答:冰完全融化时容器内的水面高度为 7.4 cm。 [解析]
(1)原来水柱只有 4.4 cm,因为“水面上升到 5.5 cm 处”说明了冰柱插入水中水面上升了$(5.5 - 4.4)cm$,用底面积乘以上升的水 1.1 cm 的高度,就是$\frac{1}{3}$冰柱的体积,再求整个冰柱的体积即可。
(2)根据“冰化成水,体积减少原来的$\frac{1}{11}$”,把冰的体积看作单位“1”,则水是原来冰柱的$(1 - \frac{1}{11})$,再根据求一个数的几分之几是多少用乘法求出融化后水的体积,然后除以容器的底面积,即可求出全部融化后增加的高度,进而求出冰柱完全融化时容器内的水面高度。
(1)$10×10×(5.5 - 4.4)÷\frac{1}{3}=330(cm^{3})$
 答:冰柱的体积为$330 cm^{3}$。
答:冰柱的体积为$330 cm^{3}$。 (2)冰融化成水的体积为$330×(1 - \frac{1}{11})=300(cm^{3})$ $300÷(10×10)+4.4 = 7.4(cm)$ 答:冰完全融化时容器内的水面高度为 7.4 cm。 [解析]
(1)原来水柱只有 4.4 cm,因为“水面上升到 5.5 cm 处”说明了冰柱插入水中水面上升了$(5.5 - 4.4)cm$,用底面积乘以上升的水 1.1 cm 的高度,就是$\frac{1}{3}$冰柱的体积,再求整个冰柱的体积即可。
(2)根据“冰化成水,体积减少原来的$\frac{1}{11}$”,把冰的体积看作单位“1”,则水是原来冰柱的$(1 - \frac{1}{11})$,再根据求一个数的几分之几是多少用乘法求出融化后水的体积,然后除以容器的底面积,即可求出全部融化后增加的高度,进而求出冰柱完全融化时容器内的水面高度。
查看更多完整答案,请扫码查看


