《2025年单元双测全优测评卷九年级数学下册苏科版》

17.(2024·武汉中考)抛物线 $y = ax^{2}+bx + c(a、b、c$是常数，$a＜0)$经过$( - 1,1)$、$(m,1)$两点，且 $0＜m＜1$. 下列四个结论：①$b＞0$；②若 $0＜x＜1$，则 $a(x - 1)^{2}+b(x - 1)+c＞1$；③若 $a = - 1$，则关于 $x$的一元二次方程 $ax^{2}+bx + c = 2$无实数解；④点 $A(x_{1},y_{1})$、$B(x_{2},y_{2})$在抛物线上，若 $x_{1}+x_{2}＞-\frac{1}{2}$，$x_{1}＞x_{2}$，总有 $y_{1}＜y_{2}$，则 $0＜m\leqslant\frac{1}{2}$. 其中正确的是_______.(填写序号)

答案： ②③④ [解析]
∵y = ax² + bx + c(a、b、c是常数，a＜0)经过(-1,1)、(m,1)两点，且0＜m＜1，
∴对称轴为直线x = -$\frac{b}{2a}$=$\frac{-1 + m}{2}$.
∵-$\frac{1}{2}$＜$\frac{-1 + m}{2}$＜0，
∴x = -$\frac{b}{2a}$＜0.
∵a＜0，
∴b＜0. 故①错误.
∵抛物线y = ax² + bx + c经过(-1,1)、(m,1)，
∴当-1＜x＜m时，y = ax² + bx + c＞1.
∵0＜x＜1，
∴-1＜x - 1＜0.
又0＜m＜1，
∴若0＜x＜1，则a(x - 1)² + b(x - 1)+c＞1，故②正确.
由①可得-$\frac{1}{2}$＜$\frac{-1 + m}{2}$=-$\frac{b}{2a}$=$\frac{b}{2}$＜0，
∴-$\frac{1}{2}$＜$\frac{b}{2}$＜0，即-1＜b＜0.
当a = -1时，抛物线表达式为y = -x² + bx + c，
设顶点纵坐标为t = $\frac{4ac - b²}{4a}$=$\frac{-4c - b²}{-4}$.
∵抛物线y = -x² + bx + c(a、b、c是常数，a＜0)经过(-1,1)，
∴-1 - b + c = 1，
∴c = b + 2，
∴t = $\frac{-4c - b²}{-4}$=$\frac{b² + 4c}{4}$=$\frac{1}{4}$b² + c=$\frac{1}{4}$b² + b + 2=$\frac{1}{4}$(b + 2)² + 1.
∵-1＜b＜0，$\frac{1}{4}$＞0，
∴当b = 0时，t = 2，而b＜0，
∴关于x的一元二次方程ax² + bx + c = 2无解，故③正确.
∵a＜0，抛物线开口向下，点A(x₁,y₁)、B(x₂,y₂)在抛物线上，x₁ + x₂＞-$\frac{1}{2}$，x₁＞x₂，总有y₁＜y₂，
∴$\frac{x₁ + x₂}{2}$＞-$\frac{1}{4}$，
∴点A(x₁,y₁)离x = $\frac{-1 + m}{2}$较远，
∴-$\frac{1}{2}$＜$\frac{-1 + m}{2}$≤-$\frac{1}{4}$，解得0＜m≤$\frac{1}{2}$，故④正确. 综上，正确的是②③④.

18. 中考新考法 规律探究 如图，一段抛物线 $y = - x(x - 1)(0\leqslant x\leqslant1)$记为 $m_{1}$，它与 $x$轴交点为 $O$、$A_{1}$，顶点为 $P_{1}$；将 $m_{1}$绕点 $A_{1}$旋转180°得 $m_{2}$，交 $x$轴于点 $A_{2}$，顶点为 $P_{2}$；将 $m_{2}$绕点 $A_{2}$旋转180°得 $m_{3}$，交 $x$轴于点 $A_{3}$，顶点为 $P_{3}$，…，如此进行下去，直至得 $m_{10}$，顶点为 $P_{10}$，则 $P_{10}$的坐标为_______.

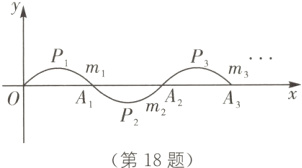
答案： ($\frac{19}{2}$,-$\frac{1}{4}$) [解析]y = -x(x - 1)=-(x - $\frac{1}{2}$)²+$\frac{1}{4}$(0≤x≤1)，
∴P₁的坐标为($\frac{1}{2}$,$\frac{1}{4}$).
∵OA₁ = A₁A₂ = 1，P₂P₄ = P₁P₃ = 2，
∴P₂的横坐标是$\frac{1 + 2}{2}$=$\frac{3}{2}$，纵坐标是-$\frac{1}{4}$，即P₂的坐标为($\frac{3}{2}$,-$\frac{1}{4}$)，
∴P₁₀的横坐标是$\frac{9 + 10}{2}$=$\frac{19}{2}$，纵坐标是-$\frac{1}{4}$，即P₁₀的坐标为($\frac{19}{2}$,-$\frac{1}{4}$).

19.(6分)教材P22习题T1·变式 已知二次函数 $y = x^{2}+ax + 3$的图像经过点 $P( - 2,3)$.
(1)求 $a$的值和图像的顶点坐标；
(2)点 $Q(m,n)$在该二次函数的图像上，当 $m = 2$时，求 $n$的值.

答案：
(1)把点P(-2,3)代入y = x² + ax + 3，得a = 2，
∴y = x² + 2x + 3=(x + 1)² + 2.
∴图像的顶点坐标为(-1,2).
(2)
∵Q(m,n)在该二次函数图像上，
∴当m = 2时，n = 2² + 2×2 + 3 = 11.

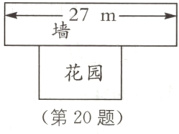
20.(6分)如图，用一段长为45 m的篱笆围成一个一边靠墙的矩形花园，墙长为27 m，设花园的面积为 $S\ m^{2}$，平行于墙的边长为 $x\ m$. 若 $x$不小于17 m.
(1)求出 $S$关于 $x$的函数关系式；
(2)求 $S$的最大值与最小值.

答案：
(1)由题意，得平行于墙的边为x m，矩形花园的面积为S m²，则垂直于墙的一边长为$\frac{1}{2}$(45 - x)m，
根据题意，得S = $\frac{1}{2}$x(45 - x)=-$\frac{1}{2}$x²+$\frac{45}{2}$x(17≤x≤27).
(2)S = -$\frac{1}{2}$x²+$\frac{45}{2}$x = -$\frac{1}{2}$(x² - 45x)=-$\frac{1}{2}$·(x - $\frac{45}{2}$)²+$\frac{2025}{8}$(17≤x≤27).
∵17≤x≤27，a = -$\frac{1}{2}$＜0，
∴当x = $\frac{45}{2}$时，S取得最大值，此时S = $\frac{2025}{8}$.
∵$\vert27 - \frac{45}{2}\vert＜\vert17 - \frac{45}{2}\vert$，
∴当x = 17时，S取得最小值，此时S = 238.
故S的最大值是$\frac{2025}{8}$，最小值是238.