2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21.(6分)如图,在△ABC中,点D在边AB上,点E在线段CD上,且∠ACD = ∠B = ∠BAE.
(1)求证:$\frac{AD}{BC}=\frac{DE}{AC}$;
(2)当点E为CD中点时,求证:$\frac{AE^{2}}{CE^{2}}=\frac{AB}{AD}$.
(1)求证:$\frac{AD}{BC}=\frac{DE}{AC}$;
(2)当点E为CD中点时,求证:$\frac{AE^{2}}{CE^{2}}=\frac{AB}{AD}$.
答案:
(1)
∵∠ACD = ∠B = ∠BAE,∠BAC = ∠BAE + ∠CAE,∠AED = ∠BAC + ∠CAE,
∴∠AED = ∠BAC.
∵∠DAE = ∠B,
∴△AED∽△BAC,
∴$\frac{AD}{BC}=\frac{DE}{AC}$.
(2)
∵∠ADE = ∠CDA,∠DAE = ∠DCA,
∴△DAE∽△DCA,
∴$\frac{AE}{AC}=\frac{DE}{AD}$.
∵DE = EC,
∴$\frac{AE}{CE}=\frac{AC}{AD}$,
∴$\frac{AE^{2}}{CE^{2}}=\frac{AC^{2}}{AD^{2}}$.
∵∠DAC = ∠BAC,∠ACD = ∠B,
∴△ACD∽△ABC,
∴$AC^{2}=AD\cdot AB$.
∴$\frac{AE^{2}}{CE^{2}}=\frac{AD\cdot AB}{AD^{2}}=\frac{AB}{AD}$.
(1)
∵∠ACD = ∠B = ∠BAE,∠BAC = ∠BAE + ∠CAE,∠AED = ∠BAC + ∠CAE,
∴∠AED = ∠BAC.
∵∠DAE = ∠B,
∴△AED∽△BAC,
∴$\frac{AD}{BC}=\frac{DE}{AC}$.
(2)
∵∠ADE = ∠CDA,∠DAE = ∠DCA,
∴△DAE∽△DCA,
∴$\frac{AE}{AC}=\frac{DE}{AD}$.
∵DE = EC,
∴$\frac{AE}{CE}=\frac{AC}{AD}$,
∴$\frac{AE^{2}}{CE^{2}}=\frac{AC^{2}}{AD^{2}}$.
∵∠DAC = ∠BAC,∠ACD = ∠B,
∴△ACD∽△ABC,
∴$AC^{2}=AD\cdot AB$.
∴$\frac{AE^{2}}{CE^{2}}=\frac{AD\cdot AB}{AD^{2}}=\frac{AB}{AD}$.
22.(6分)(2023·绍兴中考)如图,AB是⊙O的直径,C是⊙O上一点,过点C作⊙O的切线CD,交AB的延长线于点D,过点A作AE⊥CD于点E.
(1)若∠EAC = 25°,求∠ACD的度数;
(2)若OB = 2,BD = 1,求CE的长.
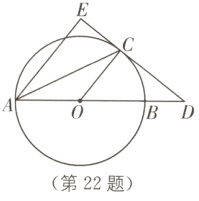
(1)若∠EAC = 25°,求∠ACD的度数;
(2)若OB = 2,BD = 1,求CE的长.

答案:
(1)
∵AE⊥ED于点E,
∴∠AEC = 90°,
∴∠ACD = ∠AEC + ∠EAC = 90° + 25° = 115°.
(2)
∵CD是⊙O的切线,
∴半径OC⊥DE,
∴∠OCD = 90°.
∵OC = OB = 2,BD = 1,
∴OD = OB + BD = 3,
∴CD = $\sqrt{OD^{2}-OC^{2}}=\sqrt{5}$.
∵∠OCD = ∠AEC = 90°,
∴OC//AE,
∴$\frac{CD}{CE}=\frac{OD}{OA}$,
∴$\frac{\sqrt{5}}{CE}=\frac{3}{2}$,
∴CE = $\frac{2\sqrt{5}}{3}$.
(1)
∵AE⊥ED于点E,
∴∠AEC = 90°,
∴∠ACD = ∠AEC + ∠EAC = 90° + 25° = 115°.
(2)
∵CD是⊙O的切线,
∴半径OC⊥DE,
∴∠OCD = 90°.
∵OC = OB = 2,BD = 1,
∴OD = OB + BD = 3,
∴CD = $\sqrt{OD^{2}-OC^{2}}=\sqrt{5}$.
∵∠OCD = ∠AEC = 90°,
∴OC//AE,
∴$\frac{CD}{CE}=\frac{OD}{OA}$,
∴$\frac{\sqrt{5}}{CE}=\frac{3}{2}$,
∴CE = $\frac{2\sqrt{5}}{3}$.
查看更多完整答案,请扫码查看


