《2025年单元双测全优测评卷九年级数学下册苏科版》

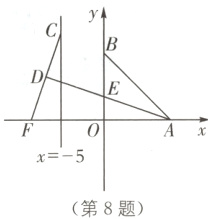
8.(2024·南通启东二模)如图，已知A、B两点的坐标分别为(8，0)、(0，8)，点C、F分别是直线x = -5和x轴上的动点，CF = 10，点D是线段CF的中点，连接AD交y轴于点E，当△ABE面积取得最小值时，sin∠BAD的值是( ).

A. $\frac{8}{17}$
B. $\frac{7}{17}$
C. $\frac{4\sqrt{2}}{13}$
D. $\frac{7\sqrt{2}}{26}$

答案： D [解析]如图，设直线x = - 5交x轴于点K，连接KD. 由题意，得KD = $\frac{1}{2}$CF = 5，
∴点D的运动轨迹是以K为圆心，5为半径的圆，
∴当直线AD与⊙K相切时，△ABE的面积最小.
∵AD是切线，点D是切点，
∴AD⊥KD.
∵AK = 13，DK = 5，
∴AD = 12.
∵tan∠EAO = $\frac{OE}{OA}$ = $\frac{DK}{AD}$，
∴$\frac{OE}{8}$ = $\frac{5}{12}$，
∴OE = $\frac{10}{3}$，
∴AE = $\sqrt{OE^{2}+OA^{2}}$ = $\frac{26}{3}$. 作EH⊥AB于H.
∵S△ABE = $\frac{1}{2}$AB·EH = S△AOB - S△AOE，
∴EH = $\frac{7\sqrt{2}}{3}$，
∴sin∠BAD = $\frac{EH}{AE}$ = $\frac{\frac{7\sqrt{2}}{3}}{\frac{26}{3}}$ = $\frac{7\sqrt{2}}{26}$. 故选D.

9.原创素养题 运算能力 在Rt△ABC中，∠C = 90°，a、b、c分别是∠A、∠B、∠C的对边，若4a = 3b，则sin B的值是________.

答案： $\frac{4}{5}$

10.(2023·扬州高邮模拟)若三角形两边为6和8，这两边的夹角为60°，则其面积为________.

答案： 12$\sqrt{3}$

11.如图，在网格中，每个小正方形的边长均为1，每个小正方形的顶点称为格点.点A、B、C三点都在格点上，则sin∠ABC = ________.

答案： $\frac{\sqrt{2}}{2}$

12.已知tan(α + 15°) = $\sqrt{3}$，则tan α的值为________.

答案： 1

13.(2024·南通启东二模)如图是一个直角三角形纸片的一部分，测得∠A = 90°，∠B = 76°，AB = 10 cm，则原来的三角形纸片的面积是________cm².(结果精确到1 cm²，参考数据：sin 76°≈0.97，cos 76°≈0.24，tan 76°≈4.01)

答案： 201 [解析]设直角三角形的另一直角边为AC，
∵∠A = 90°，∠B = 76°，AB = 10 cm，
∴tan B = $\frac{AC}{AB}$，即tan 76° = $\frac{AC}{10}$，解得AC≈40.1 cm，
∴原来的三角形纸片的面积是$\frac{1}{2}$AC·AB = $\frac{1}{2}$×40.1×10≈201(cm²).

14.(2024·常州溧阳一模)如图，在Rt△ABC中，∠ACB = 90°，BC = 2，点D在AC上，连接BD，使得BD = AC，以AC为边向外作△ACE，若CE//BD，tan E = 2，则边AE的长为________.

答案： $\sqrt{5}$ [解析]如图，过点A作AM⊥CE，垂足为M，
∵AM⊥CE，∠ACB = 90°，
∴∠ACB = ∠AMC.
∵CE//BD，
∴∠BDC = ∠ACM.
在△BCD和△AMC中，$\begin{cases}∠ACB = ∠AMC \\∠BDC = ∠ACM \\BD = AC\end{cases}$，
∴△BCD≌△AMC(AAS)，
∴AM = BC = 2.
在Rt△AME中，tan E = $\frac{AM}{ME}$ = 2，
∴ME = 1，
∴AE = $\sqrt{1^{2}+2^{2}}$ = $\sqrt{5}$.

15.新情境 架桥修路 如图，沿AB方向架桥修路，为加快施工进度，在直线AB上湖的另一边的D处同时施工.取∠ABC = 150°，BC = 1 600 m，∠BCD = 105°，则C、D两点的距离是________m.

答案： 800$\sqrt{2}$ [解析]如图，过点C作CE⊥BD，垂足为E.
∵∠ABC = 150°，
∴∠DBC = 30°，
∴∠BCE = 60°.
在Rt△BCE中，BC = 1600 m，
∴CE = $\frac{1}{2}$BC = 800 m.
∵∠BCD = 105°，
∴∠ECD = 45°.
在Rt△DCE中，
∵cos∠ECD = $\frac{CE}{CD}$，
∴CD = $\frac{CE}{cos 45°}$ = 800$\sqrt{2}$ m.

16.在△ABC中，AB = 3$\sqrt{6}$，AC = 6，∠B = 45°，则BC = ________.

答案： 3$\sqrt{3}$ + 3或3$\sqrt{3}$ - 3 [解析]①当△ABC为锐角三角形时，过点A作AD⊥BC于点D，如图
(1)，
∵AB = 3$\sqrt{6}$，∠B = 45°，
∴AD = BD = AB·sin 45° = 3$\sqrt{3}$，
∴CD = $\sqrt{AC^{2}-AD^{2}}$ = 3，
∴BC = BD + CD = 3$\sqrt{3}$ + 3；
②当△ABC为钝角三角形时，过点A作AD⊥BC交BC的延长线于点D，如图
(2)，
∵AB = 3$\sqrt{6}$，∠B = 45°，
∴AD = BD = AB·sin 45° = 3$\sqrt{3}$，
∴CD = $\sqrt{AC^{2}-AD^{2}}$ = 3，
∴BC = BD - CD = 3$\sqrt{3}$ - 3.
综上所述，BC的长为3$\sqrt{3}$ + 3或3$\sqrt{3}$ - 3.

17.(2023·广元中考)如图，在平面直角坐标系中，已知点A(1，0)、点B(0， - 3)、点C在x轴上，且点C在点A右方，连接AB、BC，若tan∠ABC = $\frac{1}{3}$，则点C的坐标为________.

答案： ($\frac{9}{4}$,0) [解析]设C(a,0)，
∴OC = a.
∵点A(1,0)，点B(0,- 3)，
∴OA = 1，AC = a - 1，OB = 3，BC = $\sqrt{3^{2}+a^{2}}$ = $\sqrt{a^{2}+9}$，
在Rt△OAB中，tan∠OBA = $\frac{OA}{OB}$ = $\frac{1}{3}$，tan∠ABC = $\frac{1}{3}$，
∴∠OBA = ∠ABC，
如图，过点C作CD//y轴交BA的延长线于点D，
∴∠OBA = ∠D，∠AOB = ∠ACD，
∴△OBA∽△CDA，∠ABC = ∠D，
∴$\frac{OB}{CD}$ = $\frac{OA}{CA}$，CD = BC，
∴$\frac{OB}{BC}$ = $\frac{OA}{AC}$，
∴$\frac{3}{\sqrt{a^{2}+9}}$ = $\frac{1}{a - 1}$，解得a = 0(舍去)或a = $\frac{9}{4}$，
∴C($\frac{9}{4}$,0).