2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
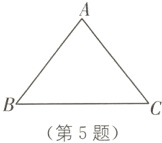
5.(2024·临夏州中考)如图,在△ABC中,AB = AC = 5,sin B = $\frac{4}{5}$,则BC的长是( ).
A. 3
B. 6
C. 8
D. 9

A. 3
B. 6
C. 8
D. 9
答案:
B [解析]过点A作BC的垂线,垂足为M,在Rt△ABM中,sin B = $\frac{AM}{AB}$,
∴AM = 5×$\frac{4}{5}$ = 4,
∴BM = $\sqrt{5^{2}-4^{2}}$ = 3. 又AB = AC,
∴BC = 2BM = 6. 故选B.
∴AM = 5×$\frac{4}{5}$ = 4,
∴BM = $\sqrt{5^{2}-4^{2}}$ = 3. 又AB = AC,
∴BC = 2BM = 6. 故选B.
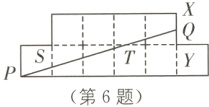
6. 10个全等的小正方形拼成如图所示的图形,点P、X、Y、S是小正方形的顶点,Q是边XY上一点,T是PQ与SY的交点. 若线段PQ恰好将这个图形分成面积相等的两个部分,则tan∠QTY的值为( ).
A. $\frac{1}{4}$
B. $\frac{8}{25}$
C. $\frac{1}{3}$
D. $\frac{2}{5}$

A. $\frac{1}{4}$
B. $\frac{8}{25}$
C. $\frac{1}{3}$
D. $\frac{2}{5}$
答案:
B [解析]如图,过点Q作QM⊥PM,交PM于点M. 设小正方形的边长为1,QY = x,则QM = QY + MY = x + 1,
∵线段PQ恰好 将这个图形分成面积相等的两个部分,
将这个图形分成面积相等的两个部分,
∴S△PQM + 1 = 10×$\frac{1}{2}$ = 5,
∴$\frac{1}{2}$PM·QM + 1 = 5,
∴$\frac{1}{2}$×5(x + 1) + 1 = 5,
∴x = $\frac{3}{5}$,
∴QM = $\frac{8}{5}$.
∵TY//PM,
∴∠QTY = ∠QPM,
∴tan∠QTY = tan∠QPM = $\frac{QM}{PM}$ = $\frac{8}{25}$. 故选B.
B [解析]如图,过点Q作QM⊥PM,交PM于点M. 设小正方形的边长为1,QY = x,则QM = QY + MY = x + 1,
∵线段PQ恰好
 将这个图形分成面积相等的两个部分,
将这个图形分成面积相等的两个部分,∴S△PQM + 1 = 10×$\frac{1}{2}$ = 5,
∴$\frac{1}{2}$PM·QM + 1 = 5,
∴$\frac{1}{2}$×5(x + 1) + 1 = 5,
∴x = $\frac{3}{5}$,
∴QM = $\frac{8}{5}$.
∵TY//PM,
∴∠QTY = ∠QPM,
∴tan∠QTY = tan∠QPM = $\frac{QM}{PM}$ = $\frac{8}{25}$. 故选B.
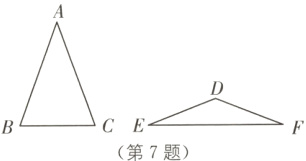
7. 如图,△ABC与△DEF都是等腰三角形,且AB = AC = 3,DE = DF = 2. 若∠B + ∠E = 90°,则△ABC与△DEF的面积比为( ).
A. 9∶4
B. 3∶2
C. $\sqrt{3}$∶$\sqrt{2}$
D. 3$\sqrt{3}$∶2$\sqrt{2}$

A. 9∶4
B. 3∶2
C. $\sqrt{3}$∶$\sqrt{2}$
D. 3$\sqrt{3}$∶2$\sqrt{2}$
答案:
A [解析]过点A作AM⊥BC,过点D作DN⊥EF.
∵△ABC与△DEF都是等腰三角形,
∴∠B = ∠C,∠E = ∠F.
∵∠B + ∠E = 90°,
∴∠B = ∠EDN.
∵S△ABC = $\frac{1}{2}$AM·BC = $\frac{1}{2}$AB·sin B·2AB·cos B = AB²sin B·cos B,S△DEF = $\frac{1}{2}$DN·EF = $\frac{1}{2}$DE·cos∠EDN·2DE·sin∠EDN = DE²sin∠EDN·cos∠EDN,
∴S△ABC : S△DEF = AB² : DE² = 9 : 4. 故选A.
∵△ABC与△DEF都是等腰三角形,
∴∠B = ∠C,∠E = ∠F.
∵∠B + ∠E = 90°,
∴∠B = ∠EDN.
∵S△ABC = $\frac{1}{2}$AM·BC = $\frac{1}{2}$AB·sin B·2AB·cos B = AB²sin B·cos B,S△DEF = $\frac{1}{2}$DN·EF = $\frac{1}{2}$DE·cos∠EDN·2DE·sin∠EDN = DE²sin∠EDN·cos∠EDN,
∴S△ABC : S△DEF = AB² : DE² = 9 : 4. 故选A.
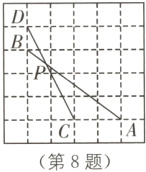
8. 如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( ).
A. $\frac{\sqrt{3}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{2}{5}$
D. $\frac{\sqrt{5}}{5}$

A. $\frac{\sqrt{3}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{2}{5}$
D. $\frac{\sqrt{5}}{5}$
答案:
B [解析]把AB向上平移一个单位到DE,连接CE,则DE//AB,
∴∠APC = ∠EDC. 在△DCE中,有EC = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$,DC = $\sqrt{4^{2}+2^{2}}$ = 2$\sqrt{5}$,DE = $\sqrt{3^{2}+4^{2}}$ = 5.
∵EC² + DC² = DE²,
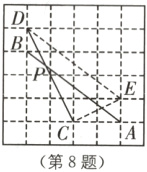
∴△DCE为直角三角形,∠DCE = 90°,
∴cos∠APC = cos∠EDC = $\frac{DC}{DE}$ = $\frac{2\sqrt{5}}{5}$. 故选B.
B [解析]把AB向上平移一个单位到DE,连接CE,则DE//AB,
∴∠APC = ∠EDC. 在△DCE中,有EC = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$,DC = $\sqrt{4^{2}+2^{2}}$ = 2$\sqrt{5}$,DE = $\sqrt{3^{2}+4^{2}}$ = 5.
∵EC² + DC² = DE²,

∴△DCE为直角三角形,∠DCE = 90°,
∴cos∠APC = cos∠EDC = $\frac{DC}{DE}$ = $\frac{2\sqrt{5}}{5}$. 故选B.
9. 教材P113问题1·变式 (2024·宜兴一模)小明沿着坡度i = 1∶2.4的斜坡向上行走了26米,则他距离地面的垂直高度升高了________米.
答案:
10 [解析]设斜坡的高为x米(x>0),则水平距离为2.4x米,则x² + (2.4x)² = 26²,解得x = 10. 故他距离地面的垂直高度升高了10米.
10.(2023·南通如皋一模)如图,在Rt△ABC中,∠ACB = 90°,tan A = $\frac{3}{5}$. 延长AB到D,使BD = $\frac{1}{2}$AB,连接CD,则tan∠BCD = ________.
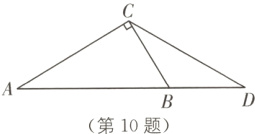

答案:
$\frac{5}{9}$ [解析]如图,过点B作BE//AC,交CD于点E,
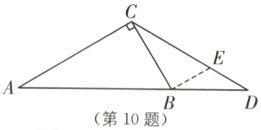
∵BE//AC,
∴$\frac{BE}{AC}$ = $\frac{BD}{AD}$,∠CBE = ∠ACB = 90°.
∵BD = $\frac{1}{2}$AB,
∴$\frac{BD}{AD}$ = $\frac{1}{3}$,
∴BE = $\frac{1}{3}$AC.
在Rt△BCE中,tan∠BCD = $\frac{BE}{BC}$ = $\frac{\frac{1}{3}AC}{BC}$,
∵tan A = $\frac{3}{5}$,
∴$\frac{BC}{AC}$ = $\frac{3}{5}$,
∴$\frac{AC}{BC}$ = $\frac{5}{3}$,
∴tan∠BCD = $\frac{1}{3}$×$\frac{5}{3}$ = $\frac{5}{9}$.
$\frac{5}{9}$ [解析]如图,过点B作BE//AC,交CD于点E,

∵BE//AC,
∴$\frac{BE}{AC}$ = $\frac{BD}{AD}$,∠CBE = ∠ACB = 90°.
∵BD = $\frac{1}{2}$AB,
∴$\frac{BD}{AD}$ = $\frac{1}{3}$,
∴BE = $\frac{1}{3}$AC.
在Rt△BCE中,tan∠BCD = $\frac{BE}{BC}$ = $\frac{\frac{1}{3}AC}{BC}$,
∵tan A = $\frac{3}{5}$,
∴$\frac{BC}{AC}$ = $\frac{3}{5}$,
∴$\frac{AC}{BC}$ = $\frac{5}{3}$,
∴tan∠BCD = $\frac{1}{3}$×$\frac{5}{3}$ = $\frac{5}{9}$.
11.(2024·上海闵行区期中)在Rt△ABC中,∠C = 90°,cos B = $\frac{5}{7}$,如果AB = 14,那么AC = ________.
答案:
4$\sqrt{6}$ [解析]
∵cos B = $\frac{5}{7}$,AB = 14,
∴cos B = $\frac{BC}{AB}$ = $\frac{BC}{14}$ = $\frac{5}{7}$,
∴BC = 10,
∴AC = $\sqrt{AB^{2}-BC^{2}}$ = $\sqrt{14^{2}-10^{2}}$ = 4$\sqrt{6}$.
∵cos B = $\frac{5}{7}$,AB = 14,
∴cos B = $\frac{BC}{AB}$ = $\frac{BC}{14}$ = $\frac{5}{7}$,
∴BC = 10,
∴AC = $\sqrt{AB^{2}-BC^{2}}$ = $\sqrt{14^{2}-10^{2}}$ = 4$\sqrt{6}$.
查看更多完整答案,请扫码查看


