2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
12.(2024·连云港期中)在△ABC中,$\sqrt{\sin A - 0.5}$ + |3tan B - 3| = 0,则△ABC是________三角形.
答案:
钝角 [解析]
∵$\sqrt{\sin A - 0.5}$ + |3tan B - 3| = 0,
∴sin A = 0.5,3tan B = 3,解得tan B = 1,
故∠A = 30°,∠B = 45°,
∴∠C = 105°,则△ABC是钝角三角形.
∵$\sqrt{\sin A - 0.5}$ + |3tan B - 3| = 0,
∴sin A = 0.5,3tan B = 3,解得tan B = 1,
故∠A = 30°,∠B = 45°,
∴∠C = 105°,则△ABC是钝角三角形.
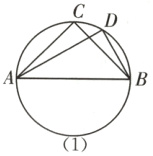
13. 已知⊙O的直径AB = 2,过点A的两条弦AC = $\sqrt{2}$,AD = $\sqrt{3}$,则∠CBD = ________.
答案:
15°或105° [解析]
∵AB为⊙O的直径,
∴∠ACB = ∠ADB = 90°.
在△ABC中,∠ACB = 90°,AB = 2,AC = $\sqrt{2}$,
∴sin∠ABC = $\frac{AC}{AB}$ = $\frac{\sqrt{2}}{2}$,
∴∠ABC = 45°.
在△ABD中,∠ADB = 90°,AB = 2,AD = $\sqrt{3}$,
∴sin∠ABD = $\frac{AD}{AB}$ = $\frac{\sqrt{3}}{2}$,
∴∠ABD = 60°.
分两种情况:
①如图
(1),当两条弦AC与AD在直径AB的同侧时,∠CBD = ∠ABD - ∠ABC = 15°;
②如图
(2),当两条弦AC与AD在直径AB的异侧时,∠CBD = ∠ABD + ∠ABC = 105°.
综上所述,∠CBD = 15°或105°.

15°或105° [解析]
∵AB为⊙O的直径,
∴∠ACB = ∠ADB = 90°.
在△ABC中,∠ACB = 90°,AB = 2,AC = $\sqrt{2}$,
∴sin∠ABC = $\frac{AC}{AB}$ = $\frac{\sqrt{2}}{2}$,
∴∠ABC = 45°.
在△ABD中,∠ADB = 90°,AB = 2,AD = $\sqrt{3}$,
∴sin∠ABD = $\frac{AD}{AB}$ = $\frac{\sqrt{3}}{2}$,
∴∠ABD = 60°.
分两种情况:
①如图
(1),当两条弦AC与AD在直径AB的同侧时,∠CBD = ∠ABD - ∠ABC = 15°;
②如图
(2),当两条弦AC与AD在直径AB的异侧时,∠CBD = ∠ABD + ∠ABC = 105°.
综上所述,∠CBD = 15°或105°.


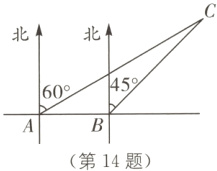
14.(2023·眉山中考)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是________海里.

答案:
6($\sqrt{3}$ + 1) [解析]如图,过点C作CH⊥AB交AB延长线于点H.
∵∠DAC = 60°,∠CBE = 45°,
∴∠CAH = 90° - ∠CAD = 30°,∠CBH = 90° - ∠CBE = 45°,
∴∠BCH = 90° - 45° = 45° = ∠CBH,
∴BH = CH.
在Rt△ACH中,∠CAH = 30°,AH = AB + BH = 12 + CH,tan 30° = $\frac{CH}{AH}$,
∴CH = $\frac{\sqrt{3}}{3}$(12 + CH),解得CH = 6($\sqrt{3}$ + 1).

6($\sqrt{3}$ + 1) [解析]如图,过点C作CH⊥AB交AB延长线于点H.
∵∠DAC = 60°,∠CBE = 45°,
∴∠CAH = 90° - ∠CAD = 30°,∠CBH = 90° - ∠CBE = 45°,
∴∠BCH = 90° - 45° = 45° = ∠CBH,
∴BH = CH.
在Rt△ACH中,∠CAH = 30°,AH = AB + BH = 12 + CH,tan 30° = $\frac{CH}{AH}$,
∴CH = $\frac{\sqrt{3}}{3}$(12 + CH),解得CH = 6($\sqrt{3}$ + 1).

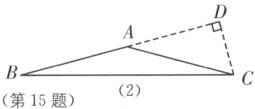
15.(2023·襄阳宜城模拟)等腰三角形腰长为8,面积为16,则底角的度数为________.
答案:
75°或15° [解析]设该等腰三角形为△ABC,其中AB = AC = 8. 设其面积为S.
如图
(1),当△ABC是锐角三角形时,过点C作边AB上的高CD,则CD = $\frac{2S}{AB}$ = $\frac{2×16}{8}$ = 4.
∵CD = $\frac{1}{2}$AC,
∴sin A = $\frac{CD}{AC}$ = $\frac{1}{2}$,
∴∠A = 30°,
∴∠B = $\frac{180° - 30°}{2}$ = 75°.
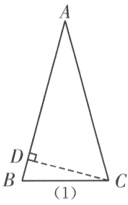
如图
(2),当△ABC是钝角三角形时,过点C作边AB上的高CD,则CD = $\frac{2S}{AB}$ = $\frac{2×16}{8}$ = 4.
∵CD = $\frac{1}{2}$AC,
∴sin∠DAC = $\frac{CD}{AC}$ = $\frac{1}{2}$,
∴∠CAD = 30°.
∵∠B = ∠ACB,
∴∠B = $\frac{1}{2}$∠CAD = 15°.
综上所述,底角的度数为75°或15°.
75°或15° [解析]设该等腰三角形为△ABC,其中AB = AC = 8. 设其面积为S.
如图
(1),当△ABC是锐角三角形时,过点C作边AB上的高CD,则CD = $\frac{2S}{AB}$ = $\frac{2×16}{8}$ = 4.
∵CD = $\frac{1}{2}$AC,
∴sin A = $\frac{CD}{AC}$ = $\frac{1}{2}$,
∴∠A = 30°,
∴∠B = $\frac{180° - 30°}{2}$ = 75°.


如图
(2),当△ABC是钝角三角形时,过点C作边AB上的高CD,则CD = $\frac{2S}{AB}$ = $\frac{2×16}{8}$ = 4.
∵CD = $\frac{1}{2}$AC,
∴sin∠DAC = $\frac{CD}{AC}$ = $\frac{1}{2}$,
∴∠CAD = 30°.
∵∠B = ∠ACB,
∴∠B = $\frac{1}{2}$∠CAD = 15°.
综上所述,底角的度数为75°或15°.
16.(2023·常州中考)如图,在Rt△ABC中,∠A = 90°,点D在边AB上,连接CD. 若BD = CD,$\frac{AD}{BD}$ = $\frac{1}{3}$,则tan B = ________.


答案:
$\frac{\sqrt{2}}{2}$ [解析]设AD = t,
∵BD = CD,$\frac{AD}{BD}$ = $\frac{1}{3}$,
∴BD = CD = 3t,
∴AC = $\sqrt{CD^{2}-AD^{2}}$ = 2$\sqrt{2}$t,AB = AD + BD = 4t,
∴tan B = $\frac{AC}{AB}$ = $\frac{2\sqrt{2}t}{4t}$ = $\frac{\sqrt{2}}{2}$.
∵BD = CD,$\frac{AD}{BD}$ = $\frac{1}{3}$,
∴BD = CD = 3t,
∴AC = $\sqrt{CD^{2}-AD^{2}}$ = 2$\sqrt{2}$t,AB = AD + BD = 4t,
∴tan B = $\frac{AC}{AB}$ = $\frac{2\sqrt{2}t}{4t}$ = $\frac{\sqrt{2}}{2}$.
17. 如图是一张宽为m的矩形台球桌ABCD,一球从点M(点M在长边CD上)出发沿虚线MN射向边BC,然后反弹到边AB上的点P. 如果MC = n,∠CMN = α,那么点P与点B的距离为________.


答案:
$\frac{m - n·\tan\alpha}{\tan\alpha}$ [解析]如图,由题意知∠NPB = ∠NMC = α. 在Rt△MNC中,MC = n,∠NMC = α,
∴NC = MC·tanα = n·tanα,
∴BN = BC - NC = m - n·tanα. 在Rt△BPN中,∠BPN = α,tanα = $\frac{BN}{PB}$,
∴PB = $\frac{BN}{\tan\alpha}$ = $\frac{m - n·\tan\alpha}{\tan\alpha}$.

$\frac{m - n·\tan\alpha}{\tan\alpha}$ [解析]如图,由题意知∠NPB = ∠NMC = α. 在Rt△MNC中,MC = n,∠NMC = α,
∴NC = MC·tanα = n·tanα,
∴BN = BC - NC = m - n·tanα. 在Rt△BPN中,∠BPN = α,tanα = $\frac{BN}{PB}$,
∴PB = $\frac{BN}{\tan\alpha}$ = $\frac{m - n·\tan\alpha}{\tan\alpha}$.

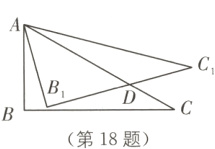
18. 如图,在Rt△ABC中,∠ABC = 90°,∠ACB = 30°,将△ABC绕点A按逆时针方向旋转15°后得到△AB₁C₁,B₁C₁交AC于点D,若AD = 2$\sqrt{2}$,则△ABC的周长等于________.

答案:
6 + 2$\sqrt{3}$ [解析]在Rt△ABC中,∠ABC = 90°,∠ACB = 30°,则∠BAC = 60°.
∵△ABC绕点A按逆时针方向旋转15°后得到△AB₁C₁,
∴∠B₁AD = 45°,∠AB₁D = 90°,故△AB₁D是等腰直角三角形. 在Rt△AB₁D中,AD = 2$\sqrt{2}$,根据勾股定理,得AB₁ = 2,所以AB = AB₁ = 2,所以AC = 2AB = 4,BC = 2$\sqrt{3}$,故△ABC的周长为AB + BC + AC = 2 + 2$\sqrt{3}$ + 4 = 6 + 2$\sqrt{3}$.
∵△ABC绕点A按逆时针方向旋转15°后得到△AB₁C₁,
∴∠B₁AD = 45°,∠AB₁D = 90°,故△AB₁D是等腰直角三角形. 在Rt△AB₁D中,AD = 2$\sqrt{2}$,根据勾股定理,得AB₁ = 2,所以AB = AB₁ = 2,所以AC = 2AB = 4,BC = 2$\sqrt{3}$,故△ABC的周长为AB + BC + AC = 2 + 2$\sqrt{3}$ + 4 = 6 + 2$\sqrt{3}$.
19.(6分)(2024·盐城中考)计算:| - 2| - (1 + π)⁰ + 4sin 30°.
答案:
原式 = 2 - 1 + 4×$\frac{1}{2}$ = 2 - 1 + 2 = 3.
查看更多完整答案,请扫码查看


