《2025年单元双测全优测评卷九年级数学下册苏科版》

25. (8分)如图是一种新型的滑梯的示意图，其中线段PA是高度为6米的平台，滑道AB是函数y = $\frac{10}{x}$的图像的一部分，滑道BCD是二次函数图像的一部分，两滑道的连接点B为抛物线的顶点，且点B到地面的距离为2米，当甲同学滑到点C时，与地面的距离为1米，与点B的水平距离CE也为1米.
(1)试求滑道BCD所在抛物线的表达式；
(2)试求甲同学从点A滑到地面上点D时，所经过的水平距离.
　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　

答案：
(1)由点B到地面的距离为2米，设点B坐标为(x,2)，代入y=$\frac{10}{x}$，得x=5，
∴B(5,2). 故设滑道BCD所在抛物线的表达式为y=a(x - 5)²+2.
∵点C与地面的距离为1米，与点B的水平距离CE也为1米，
∴C(6,1). 将C(6,1)代入，得a+2=1，解得a= - 1，故滑道BCD所在抛物线的表达式为y= - (x - 5)²+2.
(2)令y=0，解得x=5±$\sqrt{2}$，
∴D(5+$\sqrt{2}$,0). 将y=6代入y=$\frac{10}{x}$，得x=$\frac{5}{3}$，
∴5+$\sqrt{2}$ - $\frac{5}{3}$=($\frac{10}{3}$+$\sqrt{2}$)米. 故甲同学从点A滑到地面上点D时，所经过的水平距离为($\frac{10}{3}$+$\sqrt{2}$)米.

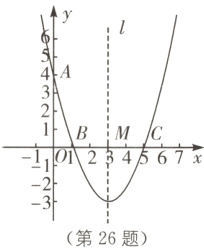
26. (8分)如图，在平面直角坐标系xOy中，已知抛物线经过点A(0，4)、B(1，0)、C(5，0)，抛物线的对称轴l与x轴相交于点M.
(1)求抛物线的表达式和对称轴.
(2)设点P为抛物线(x＞5)上的一点，若以点A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数，请你直接写出点P的坐标.
(3)连接AC，探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由.
　　　　　　　　　　　　　　　　　　

答案：

(1)根据已知条件可设抛物线的表达式为y=a(x - 1)(x - 5)，把A(0,4)代入y=a(x - 1)(x - 5)，得a=$\frac{4}{5}$，
∴y=$\frac{4}{5}$(x - 1)(x - 5)=$\frac{4}{5}$x² - $\frac{24}{5}$x+4=$\frac{4}{5}$(x - 3)² - $\frac{16}{5}$. 故抛物线的表达式为y=$\frac{4}{5}$x² - $\frac{24}{5}$x+4，对称轴是直线x=3.
(2)由题意，知以A、O、M、P为顶点的四边形有两条边AO=4，OM=3.
∵点P的横坐标大于5，
∴MP＞2，AP＞5.
∴四条边的长只能是3、4、5、6.
∵抛物线对称轴过点M，
∴PM=5，此时点P横坐标为6，即AP=6. 故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立，即点P的坐标为(6,4).
(3)在直线AC的下方的抛物线上存在点N，使△NAC的面积最大. 设点N的横坐标为t，此时点N(t,$\frac{4}{5}$t² - $\frac{24}{5}$t+4)(0＜t＜5)，如图，过点N作NG//y轴交AC于点G.

由点A(0,4)和点C(5,0)，可求出直线AC的表达式为y= - $\frac{4}{5}$x+4. 把x=t代入，得y= - $\frac{4}{5}$t+4，则G(t, - $\frac{4}{5}$t+4). 此时NG= - $\frac{4}{5}$t+4 - ($\frac{4}{5}$t² - $\frac{24}{5}$t+4)= - $\frac{4}{5}$t²+4t，
∴$S_{\triangle NAC}=\frac{1}{2}NG·OC=\frac{1}{2}$( - $\frac{4}{5}$t²+4t)×5= - 2t²+10t= - 2(t - $\frac{5}{2}$)²+$\frac{25}{2}$.
∴当t=$\frac{5}{2}$时，△NAC的面积最大，最大值为$\frac{25}{2}$. 由t=$\frac{5}{2}$，得y=$\frac{4}{5}$t² - $\frac{24}{5}$t+4= - 3，
∴N($\frac{5}{2}$, - 3).