《2025年单元双测全优测评卷九年级数学下册苏科版》

1. 下列线段中能成比例的是( ).
A. 3 cm、5 cm、7 cm、9 cm
B. 2 cm、5 cm、6 cm、8 cm
C. 3 cm、6 cm、9 cm、18 cm
D. 1 cm、3 cm、4 cm、7 cm

答案： C

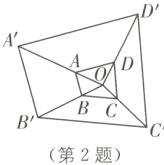
2. 如图，以点O为位似中心，作四边形ABCD的位似图形A'B'C'D'，已知$\frac{OA}{OA'}=\frac{1}{3}$，若四边形ABCD的面积是2，则四边形A'B'C'D'的面积是( ).

A. 4
B. 6
C. 16
D. 18

答案： D

3. (2024·内江中考)已知△ABC与△DEF相似，且相似比为1∶3，则△ABC与△DEF的周长之比是( ).
A. 1∶1
B. 1∶3
C. 1∶6
D. 1∶9

答案： B

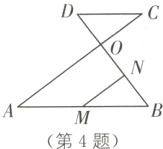
4. (2023·哈尔滨中考)如图，AC、BD相交于点O，AB//DC，M是AB的中点，MN//AC，交BD于点N，若DO∶OB = 1∶2，AC = 12，则MN的长为( ).

A. 2
B. 4
C. 6
D. 8

答案： B [解析]
∵AB//DC,
∴△CDO∽△ABO,
∴$\frac{OD}{OB}=\frac{OC}{OA}$.
∵DO:OB = 1:2,
∴$\frac{OC}{OA}=\frac{1}{2}$,
∴$OC=\frac{1}{2}OA$.
∵AC = OA + OC = 12,
∴$OA+\frac{1}{2}OA = 12$,
∴OA = 8.
∵MN//AC,M是AB的中点，
∴MN为△AOB的中位线,
∴$MN=\frac{1}{2}OA=\frac{1}{2}\times8 = 4$. 故选B.

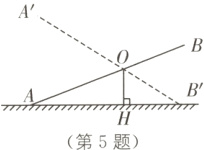
5. 教材P86习题T7·变式(2023·南京中考)如图，不等臂跷跷板AB的一端A碰到地面时，另一端B到地面的高度为60 cm；当AB的一端B碰到地面时，另一端A到地面的高度为90 cm，则跷跷板AB的支撑点O到地面的高度OH是( ).

A. 36 cm
B. 40 cm
C. 42 cm
D. 45 cm

答案：
A [解析]如图
(1),过点B作BC⊥AH,垂足为C.
　　　　　　
∵OH⊥AC,BC⊥AC,
∴∠AHO = ∠ACB = 90°.
∵∠BAC = ∠OAH,
∴△AOH∽△ABC,
∴$\frac{OH}{BC}=\frac{AO}{AB}$,
∴$\frac{OH}{60}=\frac{AO}{AB}$.
　如图
(2),过点A作AD⊥BH,垂足为D.
　　　　　　
∵OH⊥BD,AD⊥BD,
∴∠OHB = ∠ADB = 90°.
∵∠ABD = ∠OBH,
∴△ABD∽△OBH,
∴$\frac{OH}{AD}=\frac{OB}{AB}$,
∴$\frac{OH}{90}=\frac{OB}{AB}$,
∴$\frac{OH}{60}+\frac{OH}{90}=\frac{AO}{AB}+\frac{OB}{AB}$,
∴$\frac{OH}{60}+\frac{OH}{90}=\frac{AB}{AB}$,
∴$\frac{OH}{60}+\frac{OH}{90}=1$,解得OH = 36,
∴跷跷板AB的支撑点O到地面的高度OH是36cm. 故选A.

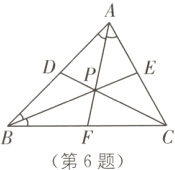
6. (2024·南京秦淮区期末)如图，△ABC的三条中线AF、BE、CD相交于点P. 以下结论：①$S_{\triangle APB}=S_{\triangle APC}$；②AP = BP；③AP = 2PF；④∠BPC = 2∠BAC. 其中，正确的结论为( ).

A. ①③
B. ②③
C. ③④
D. ①②④

答案： A [解析]
∵AF是△ABC的中线,
∴BF = CF,
∴$S_{\triangle ABF}=S_{\triangle ACF}$,$S_{\triangle PBF}=S_{\triangle PCF}$,
∴$S_{\triangle ABF}-S_{\triangle PBF}=S_{\triangle ACF}-S_{\triangle PCF}$,
　即$S_{\triangle ABP}=S_{\triangle ACP}$,故①符合题意;
　如果AP = BP,
∵CD是△ABC的中线,
∴PD⊥AB,但PD不一定垂直AB,故②不符合题意;
∵△ABC的三条中线AF、BE、CD相交于点P,
∴P是△ABC的重心,
∴AP = 2PF,故③符合题意;
　当P是△ABC的外心时,∠BPC = 2∠BAC,
∵P是△ABC的重心,不一定是△ABC的外心,
∴∠BPC不一定等于2∠BAC,故④不符合题意.
∴其中正确的结论为①③. 故选A.