《2025年单元双测全优测评卷九年级数学下册苏科版》

25.(8分)(2024·江西中考)如图，一小球从斜坡 $O$点以一定的方向弹出，球的飞行路线可以用二次函数 $y = ax^{2}+bx(a＜0)$刻画，斜坡可以用一次函数 $y = \frac{1}{4}x$刻画，小球飞行的水平距离 $x$(米)与小球飞行的高度 $y$(米)的变化规律如表：

(1)①$m =$_______，$n =$_______；
②小球的落点是 $A$，求点 $A$的坐标.
(2)小球飞行高度 $y$(米)与飞行时间 $t$(秒)满足关系：$y = - 5t^{2}+vt$.
①小球飞行的最大高度为_______米；
②求 $v$的值.

答案：
(1)①3 6 [解析]根据小球飞行的水平距离x(米)与小球飞行的高度y(米)的变化规律表可知，抛物线顶点坐标为(4,8)，
∴$\begin{cases}-\frac{b}{2a}=4 \\\frac{-b²}{4a}=8\end{cases}$，解得$\begin{cases}a = -\frac{1}{2} \\b = 4\end{cases}$，
∴二次函数表达式为y = -$\frac{1}{2}$x² + 4x.
当y = $\frac{15}{2}$时，-$\frac{1}{2}$x² + 4x = $\frac{15}{2}$，
解得x = 3或x = 5，
∴m = 3.
当x = 6时，n = y = -$\frac{1}{2}$×6² + 4×6 = 6.
②联立$\begin{cases}y = -\frac{1}{2}x² + 4x \\y = \frac{1}{4}x\end{cases}$，解得$\begin{cases}x = 0 \\y = 0\end{cases}$或$\begin{cases}x = \frac{15}{2} \\y = \frac{15}{8}\end{cases}$，
∴点A的坐标是($\frac{15}{2}$,$\frac{15}{8}$).
(2)①8 [解析]由表格可知小球飞行最大高度为8米.
②y = -5t² + vt = -5(t - $\frac{v}{10}$)²+$\frac{v²}{20}$，则$\frac{v²}{20}$=8，
解得v = 4$\sqrt{10}$(负值舍去).

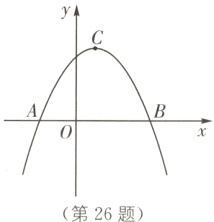
26.(8分)(2024·镇江中考)如图，在平面直角坐标系中，$O$为坐标原点，二次函数 $y = - \frac{4}{9}(x - 1)^{2}+4$的图像与 $x$轴交于 $A$、$B$两点(点 $A$在点 $B$的左侧)，顶点为 $C$.
(1)求 $A$、$B$、$C$三点的坐标.
(2)一个二次函数的图像经过 $B$、$C$、$M(t,4)$三点，其中 $t\neq1$，该函数图像与 $x$轴交于另一点 $D$，点 $D$在线段 $OB$上(与点 $O$、$B$不重合).
①若 $D$点的坐标为$(3,0)$，则 $t =$_______；
②求 $t$的取值范围；
③求 $OD\cdot DB$的最大值.

答案：
(1)
∵二次函数y = -$\frac{4}{9}$(x - 1)² + 4的图像的顶点为C，
∴C(1,4).
令y = -$\frac{4}{9}$(x - 1)² + 4 = 0，解得x = -2或x = 4，
∴A(-2,0)，B(4,0).
(2)①6 [解析]由题知，该函数过点B(4,0)、C(1,4)、D(3,0)，
∴函数表达式为y' = a(x - 4)(x - 3)，
∴函数的对称轴为直线x = $\frac{7}{2}$.
∵C(1,4)，M(t,4)，
∴点C、M关于对称轴对称，
∴$\frac{1 + t}{2}$=$\frac{7}{2}$，
∴t = 6.
②
∵点D在线段OB上，
∴DB＜OB = 4，
∴点B到对称轴的距离小于2.
设该二次函数图像的对称轴与x轴的交点坐标为(m,0)，
∵4 - m＜2，
∴m＞2.
根据对称轴的性质，得t - m = m - 1，
∴m = $\frac{t + 1}{2}$.
∵B、D两点关于对称轴对称，B(4,0)，
∴D(t - 3,0).
∵点D在线段OB上，且与端点不重合，
∴$\begin{cases}t - 3＞0 \\t - 3＜4\end{cases}$，即3＜t＜7.
∵t = 4时，过点B、C、M三点的二次函数不存在，
∴3＜t＜7且t≠4.
③
∵OD = t - 3，DB = 7 - t，
∴OD·DB=(t - 3)·(7 - t)=-t² + 10t - 21=-(t - 5)² + 4.
∵3＜t＜7且t≠4，
∴t = 5时，OD·DB有最大值，最大值为4.