2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
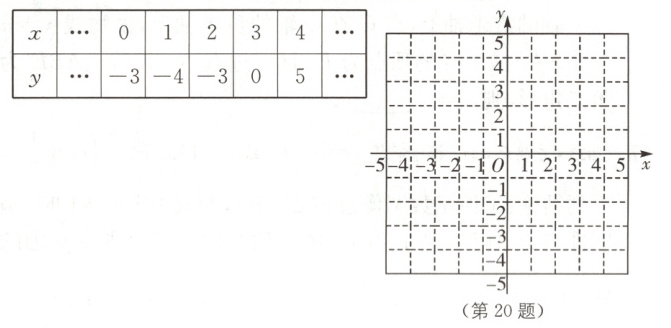
20. (6分)(2023·盐城大丰区期末)已知二次函数y = ax² + bx + c(a≠0)图像上部分点横坐标、纵坐标的对应值如表:
(1)画出函数图像,并求出二次函数的表达式;
(2)当x________时,y随x的增大而减小;
(3)当 - 1≤x≤4时,y的取值范围为________.
(1)画出函数图像,并求出二次函数的表达式;
(2)当x________时,y随x的增大而减小;
(3)当 - 1≤x≤4时,y的取值范围为________.

答案:
(1)描点、连线,画出图像如图所示.
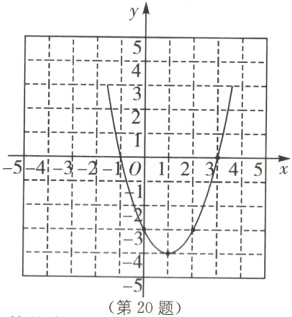
设二次函数的表达式为y=a(x - 1)² - 4.
∵二次函数经过点(3,0),
∴4a - 4=0,
∴a=1,
∴二次函数的表达式为y=(x - 1)² - 4,即y=x² - 2x - 3.
(2)<1
(3) - 4≤y≤5
(1)描点、连线,画出图像如图所示.

设二次函数的表达式为y=a(x - 1)² - 4.
∵二次函数经过点(3,0),
∴4a - 4=0,
∴a=1,
∴二次函数的表达式为y=(x - 1)² - 4,即y=x² - 2x - 3.
(2)<1
(3) - 4≤y≤5
21. (6分)(2024·扬州中考)如图,已知二次函数y = - x² + bx + c的图像与x轴交于A(-2,0)、B(1,0)两点.
(1)求b、c的值;
(2)若点P在该二次函数的图像上,且△PAB的面积为6,求点P的坐标.
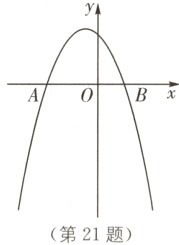
(1)求b、c的值;
(2)若点P在该二次函数的图像上,且△PAB的面积为6,求点P的坐标.

答案:
(1)二次函数y= - x²+bx+c的图像与x轴交于A( - 2,0)、B(1,0)两点,
∴$\begin{cases}-4 - 2b+c=0\\ - 1+b+c=0\end{cases}$,解得$\begin{cases}b= - 1\\c=2\end{cases}$,
∴b= - 1,c=2.
(2)由
(1)可知二次函数表达式为y= - x² - x+2,A( - 2,0)、B(1,0),
∴AB=1 - ( - 2)=3. 设P(m,n),
∴$S_{\triangle PAB}=\frac{1}{2}AB·|n|=6$,
∴|n|=4,
∴n=±4,
∴当 - x² - x+2=4时,△=1 - 8= - 7<0,无解,不符合题意,舍去;当 - x² - x+2= - 4时,x₁= - 3,x₂=2,
∴P₁( - 3, - 4),P₂(2, - 4).
(1)二次函数y= - x²+bx+c的图像与x轴交于A( - 2,0)、B(1,0)两点,
∴$\begin{cases}-4 - 2b+c=0\\ - 1+b+c=0\end{cases}$,解得$\begin{cases}b= - 1\\c=2\end{cases}$,
∴b= - 1,c=2.
(2)由
(1)可知二次函数表达式为y= - x² - x+2,A( - 2,0)、B(1,0),
∴AB=1 - ( - 2)=3. 设P(m,n),
∴$S_{\triangle PAB}=\frac{1}{2}AB·|n|=6$,
∴|n|=4,
∴n=±4,
∴当 - x² - x+2=4时,△=1 - 8= - 7<0,无解,不符合题意,舍去;当 - x² - x+2= - 4时,x₁= - 3,x₂=2,
∴P₁( - 3, - 4),P₂(2, - 4).
22. (6分)(2024·盐城东台一模)如图,抛物线y = - x² + bx + c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C.
(1)求抛物线的表达式及其对称轴;
(2)将抛物线沿y轴向下平移m(m>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,求m的值或m的取值范围.
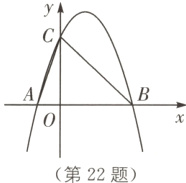
(1)求抛物线的表达式及其对称轴;
(2)将抛物线沿y轴向下平移m(m>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,求m的值或m的取值范围.

答案:
(1)
∵抛物线y= - x²+bx+c与x轴交于A( - 1,0)、B(3,0)两点,
∴$\begin{cases}-1 - b+c=0\\ - 9+3b+c=0\end{cases}$,
∴$\begin{cases}b=2\\c=3\end{cases}$,
∴抛物线的表达式为y= - x²+2x+3= - (x - 1)²+4,
∴抛物线的对称轴为直线x=1.
(2)当抛物线向下移动到过原点时,抛物线和OB有两个交点,此时0<m<3,当抛物线的顶点和x轴相切时,m=4,故当平移后的抛物线与线段OB有且只有一个交点时,0<m<3或m=4.
(1)
∵抛物线y= - x²+bx+c与x轴交于A( - 1,0)、B(3,0)两点,
∴$\begin{cases}-1 - b+c=0\\ - 9+3b+c=0\end{cases}$,
∴$\begin{cases}b=2\\c=3\end{cases}$,
∴抛物线的表达式为y= - x²+2x+3= - (x - 1)²+4,
∴抛物线的对称轴为直线x=1.
(2)当抛物线向下移动到过原点时,抛物线和OB有两个交点,此时0<m<3,当抛物线的顶点和x轴相切时,m=4,故当平移后的抛物线与线段OB有且只有一个交点时,0<m<3或m=4.
查看更多完整答案,请扫码查看


