2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21.(6分)(2024·苏州期末)在△ABC中,∠A = 30°,∠B = 105°,AB = 12.
(1)求BC的长;
(2)求△ABC的面积.(结果保留根号)
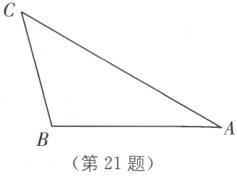
(1)求BC的长;
(2)求△ABC的面积.(结果保留根号)

答案:
(1)过点B作BH⊥AC于点H,则∠AHB = 90°.
∵∠A = 30°,AB = 12,
∴BH = $\frac{1}{2}$AB = 6.
∵∠ABC = 105°,
∴∠C = 180° - ∠A - ∠ABC = 45°.
∴△BCH是等腰直角三角形,
∴BC = $\sqrt{2}$BH = 6$\sqrt{2}$.
(2)
∵cos A = cos 30° = $\frac{AH}{AB}$ = $\frac{\sqrt{3}}{2}$,AB = 12,
∴AH = 6$\sqrt{3}$.
∵△BCH为等腰直角三角形,
∴CH = BH = 6,
∴AC = AH + CH = 6$\sqrt{3}$ + 6,
∴△ABC的面积 = $\frac{1}{2}$AC·BH = $\frac{1}{2}$×(6$\sqrt{3}$ + 6)×6 = 18$\sqrt{3}$ + 18.
(1)过点B作BH⊥AC于点H,则∠AHB = 90°.
∵∠A = 30°,AB = 12,
∴BH = $\frac{1}{2}$AB = 6.
∵∠ABC = 105°,
∴∠C = 180° - ∠A - ∠ABC = 45°.
∴△BCH是等腰直角三角形,
∴BC = $\sqrt{2}$BH = 6$\sqrt{2}$.
(2)
∵cos A = cos 30° = $\frac{AH}{AB}$ = $\frac{\sqrt{3}}{2}$,AB = 12,
∴AH = 6$\sqrt{3}$.
∵△BCH为等腰直角三角形,
∴CH = BH = 6,
∴AC = AH + CH = 6$\sqrt{3}$ + 6,
∴△ABC的面积 = $\frac{1}{2}$AC·BH = $\frac{1}{2}$×(6$\sqrt{3}$ + 6)×6 = 18$\sqrt{3}$ + 18.
22.(6分)(2023·重庆中考)为了满足市民的需求,我市在一条小河AB两侧开辟了两条长跑锻炼线路,如图:①A - D - C - B;②A - E - B.经勘测,点B在点A的正东方,点C在点B的正北方10千米处,点D在点C的正西方14千米处,点D在点A的北偏东45°方向,点E在点A的正南方,点E在点B的南偏西60°方向.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
(1)求AD的长度.(结果精确到1千米)
(2)由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?
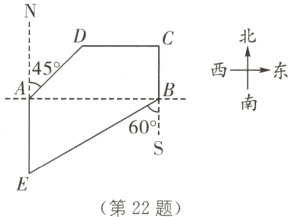
(1)求AD的长度.(结果精确到1千米)
(2)由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?

答案:
(1)如图,过点D作DF⊥AE,垂足为点F,由题意,得四边形ABCF是矩形,
∴AF = BC = 10千米.
在Rt△ADF中,∠DAF = 45°,
∴AD = $\frac{AF}{sin 45°}$ = $\frac{10}{\frac{\sqrt{2}}{2}}$ = 10$\sqrt{2}$≈10×1.41≈14(千米).
∴AD的长度约为14千米.
(2)小明应该选择线路①,
理由:在Rt△ADF中,∠DAF = 45°,AF = 10千米,
∴∠ADF = 45° = ∠DAF,
∴DF = AF = 10千米,
在Rt△ABE中,∠ABE = 90° - 60° = 30°,AB = DF + CD = 24千米,
∴AE = AB·tan 30° = 24×$\frac{\sqrt{3}}{3}$ = 8$\sqrt{3}$(千米),
EB = 2AE = 16$\sqrt{3}$千米,
按线路①A - D - C - B走的路程为AD + DC + CB = 10$\sqrt{2}$ + 14 + 10≈38(千米)
按线路②A - E - B走的路程为AE + EB = 8$\sqrt{3}$ + 16$\sqrt{3}$≈24×1.73 = 41.52(千米)
∵38千米<41.52千米,
∴小明应该选择线路①.
(1)如图,过点D作DF⊥AE,垂足为点F,由题意,得四边形ABCF是矩形,
∴AF = BC = 10千米.
在Rt△ADF中,∠DAF = 45°,
∴AD = $\frac{AF}{sin 45°}$ = $\frac{10}{\frac{\sqrt{2}}{2}}$ = 10$\sqrt{2}$≈10×1.41≈14(千米).
∴AD的长度约为14千米.
(2)小明应该选择线路①,
理由:在Rt△ADF中,∠DAF = 45°,AF = 10千米,
∴∠ADF = 45° = ∠DAF,
∴DF = AF = 10千米,
在Rt△ABE中,∠ABE = 90° - 60° = 30°,AB = DF + CD = 24千米,
∴AE = AB·tan 30° = 24×$\frac{\sqrt{3}}{3}$ = 8$\sqrt{3}$(千米),
EB = 2AE = 16$\sqrt{3}$千米,
按线路①A - D - C - B走的路程为AD + DC + CB = 10$\sqrt{2}$ + 14 + 10≈38(千米)
按线路②A - E - B走的路程为AE + EB = 8$\sqrt{3}$ + 16$\sqrt{3}$≈24×1.73 = 41.52(千米)
∵38千米<41.52千米,
∴小明应该选择线路①.
查看更多完整答案,请扫码查看


