《2025年单元双测全优测评卷九年级数学下册苏科版》

1.(教材P42习题T1·变式)在比例尺为1：50的图纸上，长度为10cm的线段实际长为(　　　).
A. 50cm　　
　B. 500cm　　
　C. $\frac{1}{50}$cm　　
　D. $\frac{1}{500}$cm

答案： B

2. 新情境 树叶中蕴含的“黄金分割” (2024·宿迁沭阳期末)校园里一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点(AP＞PB)，如果AB的长度为10cm，那么AP的长度为(　　　).

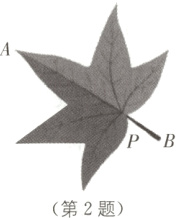
A. ($\sqrt{5}-1$)cm　　　　　　　　
　B. (2$\sqrt{5}-2$)cm
C. (5$\sqrt{5}-5$)cm　　　　　　　
　D. (10$\sqrt{5}-10$)cm

答案： C

3. 如图，∠1=∠2=∠3，则图中相似三角形共有(　　　).

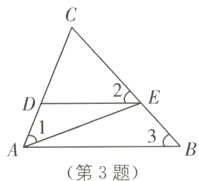
A. 3对　　　
　B. 4对　　　
　C. 5对　　　
　D. 6对

答案： B

4.(2023·绍兴中考)如图，在△ABC中，D是边BC上的点(不与点B、C重合). 过点D作DE//AB交AC于点E，过点D作DF//AC交AB于点F，N是线段BF上的点，BN = 2NF，M是线段DE上的点，DM = 2ME. 若已知△CMN的面积，则一定能求出(　　　).

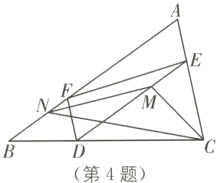
A. △AFE的面积　　　　　　
　B. △BDF的面积
C. △BCN的面积　　　　　　
　D. △DCE的面积

答案：
D　[解析]如图，连接ND,

∵DE//AB，DF//AC，
∴∠ECD = ∠FDB，∠B = ∠EDC，∠BFD = ∠A，∠A = ∠DEC.
∴△FBD∽△EDC，
∴$\frac{FB}{ED}=\frac{FD}{EC}$.
∵DM = 2ME，BN = 2NF，
∴NF = $\frac{1}{3}$BF，ME = $\frac{1}{3}$DE，
∴$\frac{NF}{ME}=\frac{BF}{DE}$，
∴$\frac{FD}{EC}=\frac{NF}{ME}$.
又∠NFD = ∠MEC，
∴△NFD∽△MEC.
∴∠ECM = ∠FDN.
∵∠FDB = ∠ECD，
∴∠MCD = ∠NDB.
∴MC//ND.
∴$S_{\triangle MNC}=S_{\triangle MDC}$.
∵DM = 2ME，
∴$S_{\triangle MEC}=\frac{1}{2}S_{\triangle DMC}=\frac{1}{2}S_{\triangle MNC}$，
∴$S_{\triangle DCE}=\frac{3}{2}S_{\triangle MNC}$. 故选D.

5.(2024·扬州梅岭中学期末)下列四条线段中，能成为成比例线段的是(　　　).
A. a = 1，b = 2，c = 3，d = 4　　
　B. a = 1，b = 2，c = 3，d = 6
C. a = 2，b = 2，c = 3，d = 4　　
　D. a = 1，b = 3，c = 4，d = 5

答案： B

6. 下列4组条件中，能判定△ABC∽△DEF的是(　　　).
A. ∠A = 45°，∠B = 55°；∠D = 45°，∠F = 75°
B. AB = 5，BC = 4，∠A = 45°；DE = 10，EF = 8，∠D = 45°
C. AB = 6，BC = 5，∠B = 40°；DE = 5，EF = 4，∠E = 40°
D. BC = 4，AC = 6，AB = 9；DE = 18，EF = 8，DF = 12

答案： D　[解析]A.
∵∠A = 45°，∠B = 55°；∠D = 45°，∠F = 75°，
∴∠C = 80°，
∴∠A = ∠D，但另两角不对应相等，
∴不能判定△ABC∽△DEF，故本选项错误；
B.
∵AB = 5，BC = 4，∠A = 45°；DE = 10，EF = 8，∠D = 45°，而∠A不是AB与BC的夹角，∠D不是DE与EF的夹角，
∴不能判定△ABC∽△DEF，故本选项错误；
C.
∵AB = 6，BC = 5，∠B = 40°；DE = 5，EF = 4，∠E = 40°，
∴$\frac{AB}{DE}\neq\frac{BC}{EF}$，
∴不能判定△ABC∽△DEF，故本选项错误；
D.
∵BC = 4，AC = 6，AB = 9；DE = 18，EF = 8，DF = 12，
∴$\frac{BC}{EF}=\frac{AC}{DF}=\frac{AB}{DE}=\frac{1}{2}$，
∴△ABC∽△DEF，故本选项正确.