《2025年单元双测全优测评卷九年级数学下册苏科版》

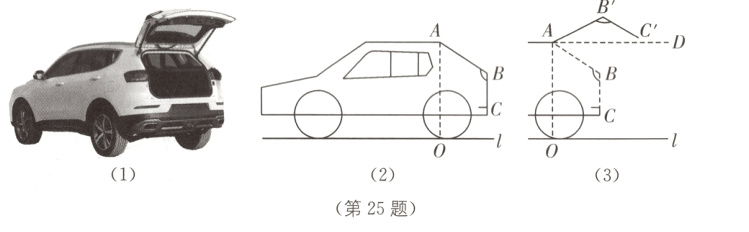
25.(8分)新情境 越野车后备箱 (2023·济南中考)如图(2)是某越野车的侧面示意图，折线段ABC表示车后盖，已知AB = 1 m，BC = 0.6 m，∠ABC = 123°，该车的高度AO = 1.7 m. 如图(3)，打开后备箱，车后盖ABC落在AB'C'处，AB'与水平面的夹角∠B'AD = 27°.
(1)求打开后备箱后，车后盖最高点B'到地面l的距离.
(2)若小琳爸爸的身高为1.8 m，他从打开的车后盖C'处经过，有没有碰头的危险？请说明理由.(结果精确到0.01 m，参考数据：sin 27°≈0.454，cos 27°≈0.891，tan 27°≈0.510，$\sqrt{3}$≈1.732)

答案：
(1)如图
(1)，作B'E⊥AD，垂足为E，
在Rt△AB'E中，∠B'AD = 27°，AB' = AB = 1 m，
∴sin 27° = $\frac{B'E}{AB'}$，
∴B'E = AB'sin 27°≈1×0.454 = 0.454(m).
∵平行线间的距离处处相等，
∴B'E + AO = 0.454 + 1.7 = 2.154≈2.15(m).
故车后盖最高点B'到地面的距离为2.15 m.
(2)没有危险. 理由如下：
如图
(2)，过点C'作C'F⊥B'E，垂足为F.
∵∠B'AD = 27°，∠B'EA = 90°，
∴∠AB'E = 63°.
∵∠AB'C' = ∠ABC = 123°，
∴∠C'B'F = ∠AB'C' - ∠AB'E = 60°，
在Rt△B'C'F中，B'C' = BC = 0.6 m，
∴B'F = B'C'·cos 60° = 0.3(m).
∵平行线间的距离处处相等，
∴C'到地面的距离为2.15 - 0.3 = 1.85(m).
∵1.85＞1.8.
∴没有危险.

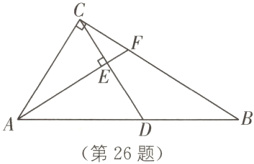
26.(8分)如图，在Rt△ABC中，∠ACB = 90°，AB = 5，sin∠CAB = $\frac{4}{5}$，D是斜边AB上一点，过点A作AE⊥CD，垂足为E，AE的延长线交BC于点F.
(1)当tan∠BCD = $\frac{1}{2}$时，求线段BF的长；
(2)当BF = $\frac{5}{4}$时，求线段AD的长.

答案：
(1)在△ABC中，∠ACB = 90°，AB = 5，
sin∠CAB = $\frac{4}{5}$，
∴BC = 4，AC = 3.
∵AE⊥CD，∠ACB = 90°，
∴∠BCD + ∠AFC = 90°，∠AFC + ∠CAF = 90°，
∴∠CAF = ∠BCD.
∴tan∠CAF = tan∠BCD = $\frac{1}{2}$.
又∠ACB = 90°，AC = 3，
∴CF = $\frac{3}{2}$，
∴BF = $\frac{5}{2}$.
(2)①如图
(1)，当点F在线段BC上时，过点B作BG//AC，交CD的延长线于点G.
∵tan∠CAF = tan∠BCD，
∴$\frac{CF}{AC}$ = $\frac{BG}{BC}$，即$\frac{4 - \frac{5}{4}}{3}$ = $\frac{BG}{4}$，
∴BG = $\frac{11}{3}$.
∵BG//AC，
∴∠ACD = ∠G，∠CAD = ∠DBG.
∴△BGD∽△ACD，
∴$\frac{BG}{AC}$ = $\frac{BD}{AD}$，
即$\frac{\frac{11}{3}}{3}$ = $\frac{5 - AD}{AD}$，
∴AD = $\frac{9}{4}$.
②如图
(2)，当点F在CB延长线上时，过点B作BG//AC，交CD的延长线于点G.
∵tan∠CAF = tan∠BCD，
∴$\frac{CF}{AC}$ = $\frac{BG}{BC}$，即$\frac{4+\frac{5}{4}}{3}$ = $\frac{BG}{4}$，
∴BG = 7.
∵BG//AC，
∴∠ACD = ∠G，∠CAD = ∠DBG.
∴△BGD∽△ACD.
∴$\frac{BG}{AC}$ = $\frac{BD}{AD}$，即$\frac{7}{3}$ = $\frac{5 - AD}{AD}$，
∴AD = $\frac{3}{2}$.
综上所述，线段AD的长为$\frac{9}{4}$或$\frac{3}{2}$.