《2025年单元双测全优测评卷九年级数学下册苏科版》

1.(2023·宿迁沭阳期末)下列函数中，二次函数是( ).
A. $y = 8x^{2}$
B. $y = 8x + 1$
C. $y = - 8x$
D. $y = - \frac{8}{x}$

答案： A

2. 教材P35复习题T4·变式 若二次函数 $y = (x - m)^{2}-1$. 当 $x\leqslant1$时，$y$随 $x$的增大而减小，则 $m$的取值范围是( ).
A. $m = 1$
B. $m＞1$
C. $m\geqslant1$
D. $m\leqslant1$

答案： C

3. 二次函数 $y = a(x - 1)^{2}+k$与 $x$轴的一个交点坐标为$( - 2,0)$，则与 $x$轴的另一个交点坐标为( ).
A. $(0,0)$
B. $(2,0)$
C. $(3,0)$
D. $(4,0)$

答案： D

4. 二次函数 $y = a(x + k)^{2}+k$，无论 $k$为何实数，其图像的顶点都在( ).
A. 直线 $y = x$上
B. 直线 $y = - x$上
C. $x$轴上
D. $y$轴上

答案： B [解析]
∵y=a(x + k)² + k，
∴二次函数的顶点坐标为(-k,k).
∴其图像顶点在直线y = -x上. 故选B.

5. 若二次函数 $y = ax^{2}+bx + c(a\neq0)$的图像如图所示，则一次函数 $y = ax + b$与反比例函数 $y = - \frac{c}{x}$在同一平面直角坐标系内的大致图像为( ).

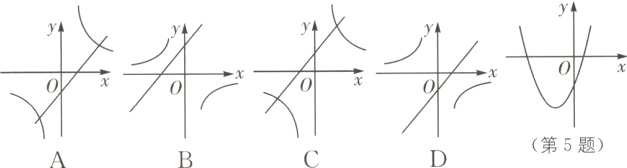
答案： C [解析]
∵抛物线开口向上，
∴a＞0.
∵抛物线对称轴在y轴左侧，
∴b＞0.
∵抛物线与y轴交点在x轴下方，
∴c＜0.
∴直线y = ax + b经过第一、二、三象限，反比例函数y = - $\frac{c}{x}$图像位于第一、三象限. 故选C.

6.(2023·日照中考)在平面直角坐标系 $xOy$中，抛物线 $y = ax^{2}+bx(a\neq0)$，满足$\begin{cases}3a + b＞0\\a + b＜0\end{cases}$，已知点$( - 3,m)$、$(2,n)$、$(4,t)$在该抛物线上，则 $m$、$n$、$t$的大小关系为( ).
A. $t\lt n\lt m$
B. $m\lt t\lt n$
C. $n\lt t\lt m$
D. $n\lt m\lt t$

答案： C [解析]
∵3a + b＞0，
∴2a + a + b＞0.
∵a + b＜0，
∴2a＞0，
∴a＞0，
∴抛物线开口向上.
∵-3a＜b＜-a，
∴$\frac{1}{2}$＜-$\frac{b}{2a}$＜$\frac{3}{2}$.
∵点(-3,m)、(2,n)、(4,t)在该抛物线上，
∴m、n、t的大小关系为n＜t＜m. 故选C.

7.(2024·南通海安一模)设函数 $y = a(x + m)^{2}+n(a\neq0,m、n$是实数$)$，当 $x = 1$时，$y = 1$；当 $x = 6$时，$y = 6$. 则( ).
A. 若 $m = - 3$，则 $a＜0$
B. 若 $m = - 4$，则 $a＞0$
C. 若 $m = - 5$，则 $a＜0$
D. 若 $m = - 6$，则 $a＞0$

答案： C [解析]由所给函数表达式可知，抛物线的对称轴为直线x = -m.
当m = -3时，抛物线的对称轴为直线x = 3，
因为(1,1)和(6,6)在抛物线上，
所以点(1,1)关于直线x = 3的对称点为(5,1).
因为6＞5,6＞1，
所以在对称轴的右侧y随x的增大而增大，则抛物线的开口向上，即a＞0.
故A选项不符合题意.
当m = -4时，抛物线的对称轴为直线x = 4，所以点(1,1)关于直线x = 4的对称点为(7,1).
因为6＜7,6＞1，所以在对称轴的右侧y随x的增大而减小，则抛物线的开口向下，即a＜0.
故B选项不符合题意.
当m = -5时，抛物线的对称轴为直线x = 5，所以点(1,1)关于直线x = 5的对称点为(9,1).
因为6＜9,6＞1，所以在对称轴的右侧y随x的增大而减小，则抛物线的开口向下，即a＜0.
故C选项符合题意.
当m = -6时，抛物线的对称轴为直线x = 6，
因为6＞1，所以顶点的纵坐标为抛物线上所有点纵坐标中最大的，则抛物线的开口向下，即a＜0.
故D选项不符合题意. 故选C.

8. 已知抛物线 $y = a(x - 3)^{2}+\frac{25}{4}$过点 $C(0,4)$，顶点为 $M$，与 $x$轴交于 $A$、$B$两点. 如图所示以 $AB$为直径作圆，记作$\odot D$，下列结论：①抛物线的对称轴是直线 $x = 3$；②点 $C$在$\odot D$外；③在抛物线上存在一点 $E$，能使四边形 $ADEC$为平行四边形；④直线 $CM$与$\odot D$相切. 正确的结论是( ).

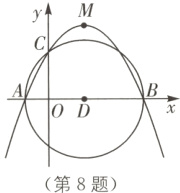
A. ①③
B. ①④
C. ③④
D. ①②③④

答案：
B [解析]由抛物线y = a(x - 3)²+$\frac{25}{4}$可知，抛物线的对称轴是直线x = 3. 故①正确；
∵抛物线y = a(x - 3)²+$\frac{25}{4}$过点C(0,4)，
∴4 = 9a+$\frac{25}{4}$，解得a = -$\frac{1}{4}$，
∴抛物线的表达式为y = -$\frac{1}{4}$(x - 3)²+$\frac{25}{4}$.
令y = 0，则-$\frac{1}{4}$(x - 3)²+$\frac{25}{4}$=0，
解得x = 8或x = -2，
∴A(-2,0)，B(8,0)，
∴AB = 10，
∴AD = 5，
∴OD = 3.
∵C(0,4)，
∴CD = $\sqrt{OC^{2}+OD^{2}}$=5.
∴CD = AD，
∴点C在圆上. 故②错误；
如图，过点C作CE//AB，交抛物线于点E.

∵将y = 4代入y = -$\frac{1}{4}$(x - 3)²+$\frac{25}{4}$，得4 = -$\frac{1}{4}$(x - 3)²+$\frac{25}{4}$，解得x = 0或x = 6，
∴CE = 6，
∴AD≠CE.
∴四边形ADEC不是平行四边形. 故③错误；
由抛物线y = a(x - 3)²+$\frac{25}{4}$可知M(3,$\frac{25}{4}$).
∵C(0,4)，
∴CM²=(3 - 0)²+($\frac{25}{4}$ - 4)²=$\frac{225}{16}$.
∵DM²=($\frac{25}{4}$)²=$\frac{625}{16}$，CM²+CD²=$\frac{225}{16}$+25=$\frac{625}{16}$，
∴CM²+CD²=DM².
∴CM⊥CD.
∴直线CM与⊙D相切. 故④正确. 故选B.