《2025年单元双测全优测评卷九年级数学下册苏科版》

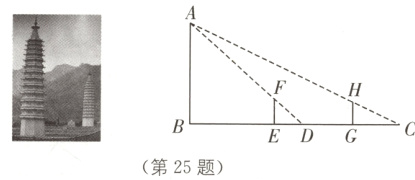
25. (8分)传统文化 拜寺口双塔(2023·攀枝花中考)拜寺口双塔，分为东西两塔，位于宁夏回族自治区银川市贺兰县拜寺口内，是保存最为完整的西夏佛塔，已有近1 000年历史，是中国佛塔建筑史上不可多得的艺术珍品. 某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理，来测量东塔的高度. 东塔的高度为AB，选取与塔底B在同一水平地面上的E、G两点，分别垂直地面竖立两根高为1.5 m的标杆EF和GH，两标杆间隔EG为46 m，并且东塔AB、标杆EF和GH在同一竖直平面内. 从标杆EF后退2 m到D处(即ED = 2 m)，从D处观察A点，A、F、D在同一直线上；从标杆GH后退4 m到C处(即CG = 4 m)，从C处观察A点，A、H、C三点也在同一直线上，且B、E、D、G、C在同一直线上，请你根据以上测量数据，帮助兴趣小组求出东塔AB的高度.

答案： 设BD = x m,则BC = BD + DG + CG = x + 46 - 2 - 4=(x + 48)m.
　
∵AB⊥BC,EF⊥BC,
∴AB//EF,
　
∴△ABD∽△FED,
∴$\frac{EF}{AB}=\frac{DE}{BD}$,即$\frac{1.5}{AB}=\frac{2}{x}$,
　　同理可证△ABC∽△HGC,
　
∴$\frac{GH}{AB}=\frac{CG}{BC}$,即$\frac{1.5}{AB}=\frac{4}{x + 48}$,
　
∴$\frac{2}{x}=\frac{4}{x + 48}$,解得x = 48,
　　经检验,x = 48是原方程的解,
∴$\frac{1.5}{AB}=\frac{2}{48}$,
　
∴AB = 36 m. 故东塔AB的高度为36 m.

26. (8分)如图，在平行四边形ABCD中，AB = 5，BC = 10，边BC上的高AM = 4，点E为边BC上的动点(不与B、C重合)，过点E作直线AB的垂线，垂足为F，连接DE、DF.
(1)求证：△ABM∽△EBF.
(2)当点E为BC的中点时，求DE的长.
(3)设BE = x，△DEF的面积为y，求y与x之间的函数关系式，并求当x为何值时，y有最大值？最大值是多少？

答案：

(1)
∵EF⊥AB,AM是边BC上的高,
　
∴∠AMB = ∠EFB = 90°.
　　又∠B = ∠B,
∴△ABM∽△EBF.
(2)如图
(1),过点E作EN⊥AD于点N.
　　　　
　　在平行四边形ABCD中,AD//BC,
　
∵AM是边BC上的高,
∴AM⊥AD,
　
∴∠AME = ∠MAN = ∠ANE = 90°,
　
∴四边形AMEN为矩形,
∴NE = AM = 4,AN = ME.
　　在Rt△ABM中,$BM=\sqrt{AB^{2}-AM^{2}}=\sqrt{5^{2}-4^{2}}=3$.
　
∵E为BC的中点,
∴$BE=\frac{1}{2}BC = 5$,
　
∴ME = AN = 2,
∴DN = 8.
　　在Rt△DNE中,$DE=\sqrt{DN^{2}+NE^{2}}=\sqrt{8^{2}+4^{2}}=4\sqrt{5}$.
(3)如图
(2),延长FE交DC的延长线于点G.
　　　　
　
∵△ABM∽△EBF,
∴$\frac{AM}{AB}=\frac{EF}{BE}$,
　
∴$\frac{4}{5}=\frac{EF}{x}$,
∴$EF=\frac{4}{5}x$.
　
∵AB//CD,
∴∠B = ∠ECG,∠EGC = ∠BFE = 90°.
　
∵∠AMB = ∠EGC = 90°,
　
∴△ABM∽△ECG,
∴$\frac{CG}{BM}=\frac{EC}{AB}$,
　
∴$\frac{CG}{3}=\frac{10 - x}{5}$,
∴$GC=\frac{3}{5}(10 - x)$.
　
∴$DG=DC + GC=5+\frac{3}{5}(10 - x)$,
　
∴$y=\frac{1}{2}EF\cdot DG=\frac{1}{2}\times\frac{4}{5}x\times[5+\frac{3}{5}(10 - x)]$
　　$=-\frac{6}{25}x^{2}+\frac{22}{5}x=-\frac{6}{25}(x-\frac{55}{6})^{2}+\frac{121}{6}$.
　
∴当$x=\frac{55}{6}$时,y有最大值为$\frac{121}{6}$.
　　故y与x之间的函数关系式为$y=-\frac{6}{25}x^{2}+\frac{22}{5}x$,当$x=\frac{55}{6}$时,y的最大值为$\frac{121}{6}$.