《2025年单元双测全优测评卷九年级数学下册苏科版》

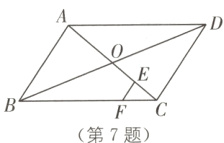
7.(2024·河南中考)如图，在□ABCD中，对角线AC、BD相交于点O，点E为OC的中点，EF//AB交BC于点F. 若AB = 4，则EF的长为(　　　).

A. $\frac{1}{2}$　　　　
　B. 1　　　　　
　C. $\frac{4}{3}$　　　　
　D. 2

答案： B　[解析]
∵四边形ABCD是平行四边形，
∴OC = OA = $\frac{1}{2}$AC.
∵点E为OC的中点，
∴CE = $\frac{1}{2}$OC = $\frac{1}{4}$AC.
∵EF//AB，
∴△CEF∽△CAB，
∴$\frac{EF}{AB}=\frac{CE}{AC}$，即$\frac{EF}{4}=\frac{1}{4}$，
∴EF = 1. 故选B.

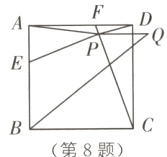
8.(2023·无锡新吴区二模)如图，在正方形ABCD中，AB = 4，E、F分别是边AB、AD上的动点，AE = DF，连接DE、CF交于点P，过点P作PQ//BC，且PQ = 2，下列结论：①DE = CF；②AE² = FP·FC；③在运动过程中，线段AP的最小值为2$\sqrt{5}-2$；④当∠CBQ的度数最大时，BQ的长为2$\sqrt{10}$. 其中正确的结论有(　　　).

A. 1个　　　
　B. 2个　　　
　C. 3个　　　
　D. 4个

答案：
C　[解析]
∵四边形ABCD是正方形，
∴∠EAD = ∠FDC = 90°，AD = DC.
在△AED和△DFC中，$\begin{cases}AD = DC\\\angle EAD = \angle FDC\\AE = DF\end{cases}$，
∴△AED≌△DFC(SAS)，
∴DE = CF，故①正确.
∵△AED≌△DFC，
∴∠ADE = ∠DCF.
∵∠ADC = ∠ADE + ∠PDC = 90°，
∴∠DCP + ∠PDC = 90°，即∠CPD = 90°，
∴∠DPF = ∠FDC = 90°.
∵∠DFP = ∠CFD，
∴△FDP∽△FCD，
∴$\frac{FD}{FC}=\frac{FP}{FD}$，
∴$FD^{2}=FP\cdot FC$.
∵AE = DF，
∴$AE^{2}=FP\cdot FC$，故②正确.
如图，取CD的中点G，连接AG、PG，
∵∠CPD = 90°，
∴PG = $\frac{1}{2}$CD = 2.
在Rt△ADG中，AG = $\sqrt{AD^{2}+DG^{2}} = 2\sqrt{5}$.
在△APG中，AP＞AG - PG，当A、P、G三点共线时，AP有最小值，AP = AG - PG = $2\sqrt{5}-2$，故③正确.
如图，过点G作GH⊥CD且GH = 2，则PQ//HG，PQ = HG，过点H作HM⊥BC交BC的延长线于点M，
∴四边形PGHQ是平行四边形.
∵GH = PG，
∴四边形PGHQ是菱形，
∴点Q在以H为圆心，2为半径的圆弧上运动，
∴当BQ与⊙H相切时，∠CBQ的度数最大，
则BM是⊙H的切线，
∴BQ = BM = BC + CM = 4 + 2 = 6，故④错误.
∴正确的结论有3个. 故选C.

9. 教材P42习题T2·变式 若$\frac{x}{y}=2$，则$\frac{x - y}{y}=$_______.

答案： 1

10.(2023·乐山中考)如图，在平行四边形ABCD中，E是线段AB上一点，连接AC、DE交于点F. 若$\frac{AE}{EB}=\frac{2}{3}$，则$\frac{S_{\triangle ADF}}{S_{\triangle AEF}}=$_______.

答案： $\frac{5}{2}$

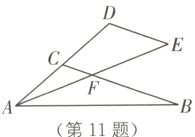
11.(2024·重庆中考)如图，在△ABC中，延长AC至点D，使CD = CA，过点D作DE//CB，且DE = DC，连接AE交BC于点F. 若∠CAB = ∠CFA，CF = 1，则BF = _______.

答案： 3

12. 中考新考法 新定义问题 实数a、n、m、b满足a＜n＜m＜b，这四个数在数轴上对应的点分别为A、N、M、B(如图)，若AM² = BM·AB，BN² = AN·AB，则称m为a、b的“大黄金数”，n为a、b的“小黄金数”，当b - a = 4时，m - n = _______.

答案： $4\sqrt{5}-8$　[解析]由题意，得AB = b - a = 4.
设AM = x，则BM = 4 - x，$x^{2}=4(4 - x)$，
解得$x_{1}=-2 + 2\sqrt{5}$，$x_{2}=-2 - 2\sqrt{5}$（舍去），则AM = BN = $2\sqrt{5}-2$，
∴MN = m - n = AM + BN - AB = 2AM - 4 = 2×($2\sqrt{5}-2$) - 4 = $4\sqrt{5}-8$.

13.(2023·无锡宜兴一模)如图，在矩形ABCD中，AB = 4，BC = 5，点E为边BC延长线一点，且CE = 3. 连接AE交边CD于点F，过点D作DH⊥AE于点H，则DH = _______.

答案： $\sqrt{5}$　[解析]
∵四边形ABCD为矩形，
∴CD//AB，DC = AB = 4，
∴∠EFC = ∠EAB.
∵∠E = ∠E，
∴△EFC∽△EAB，
∴$\frac{EC}{EB}=\frac{FC}{AB}$，
∴$\frac{3}{3 + 5}=\frac{FC}{4}$，
∴FC = 1.5，
∴DF = DC - FC = 2.5，
∴AF = $\sqrt{DF^{2}+AD^{2}}=\frac{5\sqrt{5}}{2}$.
∵∠ADC = 90°，DH⊥AE，
∴$S_{\triangle ADF}=\frac{1}{2}AD\cdot DF=\frac{1}{2}AF\cdot DH$，
∴AD·DF = AF·DH，
∴5×2.5 = $\frac{5\sqrt{5}}{2}$×DH，
∴DH = $\sqrt{5}$.