2025年单元双测全优测评卷九年级数学下册苏科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年单元双测全优测评卷九年级数学下册苏科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
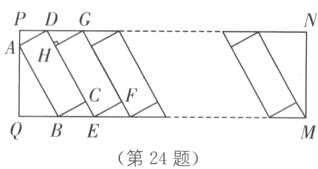
24.(10分)(2024·广东中考)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献. 为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位. 经测量,∠ABQ = 60°,AB = 5.4 m,CE = 1.6 m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定. 根据以上信息回答下列问题:(结果精确到0.1 m,参考数据$\sqrt{3}\approx1.73$)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.

答案:
(1)
∵四边形PQMN是矩形,
∴∠Q = ∠P = 90°.
在Rt△ABQ中,∠ABQ = 60°,AB = 5.4 m,
∴AQ = AB·sin∠ABQ=$\frac{27\sqrt{3}}{10}$ m,∠QAB = 30°.
∵四边形ABCD是矩形,
∴AD = BC,∠BAD = ∠BCD = ∠ABC = ∠BCE = 90°,
∴∠CBE = ∠QAB = 30°,
∴BC=$\frac{CE}{tan∠CBE}=\frac{8\sqrt{3}}{5}$ m,
∴AD=$\frac{8\sqrt{3}}{5}$ m.
∵∠PAD = 180° - 30° - 90° = 60°,
∴AP = AD·cos∠PAD=$\frac{4\sqrt{3}}{5}$ m,
∴PQ = AP + AQ=$\frac{7\sqrt{3}}{2}≈6.1$ m.
(2)在Rt△BCE中,BE=$\frac{CE}{sin∠CBE}=3.2$ m,
在Rt△ABQ中,BQ = AB·cos∠ABQ = 2.7 m.
∵该充电站有20个停车位,
∴QM = BQ + 20BE = 66.7 m.
∵四边形PQMN是矩形,
∴PN = QM = 66.7 m.
(1)
∵四边形PQMN是矩形,
∴∠Q = ∠P = 90°.
在Rt△ABQ中,∠ABQ = 60°,AB = 5.4 m,
∴AQ = AB·sin∠ABQ=$\frac{27\sqrt{3}}{10}$ m,∠QAB = 30°.
∵四边形ABCD是矩形,
∴AD = BC,∠BAD = ∠BCD = ∠ABC = ∠BCE = 90°,
∴∠CBE = ∠QAB = 30°,
∴BC=$\frac{CE}{tan∠CBE}=\frac{8\sqrt{3}}{5}$ m,
∴AD=$\frac{8\sqrt{3}}{5}$ m.
∵∠PAD = 180° - 30° - 90° = 60°,
∴AP = AD·cos∠PAD=$\frac{4\sqrt{3}}{5}$ m,
∴PQ = AP + AQ=$\frac{7\sqrt{3}}{2}≈6.1$ m.
(2)在Rt△BCE中,BE=$\frac{CE}{sin∠CBE}=3.2$ m,
在Rt△ABQ中,BQ = AB·cos∠ABQ = 2.7 m.
∵该充电站有20个停车位,
∴QM = BQ + 20BE = 66.7 m.
∵四边形PQMN是矩形,
∴PN = QM = 66.7 m.
25.(10分)中考新考法 新定义问题 (2023·宿迁中考)规定:若函数$y_{1}$的图像与函数$y_{2}$的图像有三个不同的公共点,则称这两个函数互为“兄弟函数”,其公共点称为“兄弟点”.
(1)下列三个函数①$y = x + 1$;②$y = -\frac{3}{x}$;③$y = -x^{2}+1$,其中与二次函数$y = 2x^{2}-4x - 3$互为“兄弟函数”的是_______(填写序号).
(2)若函数$y_{1}=ax^{2}-5x + 2(a\neq0)$与$y_{2}=-\frac{1}{x}$互为“兄弟函数”,x = 1是其中一个“兄弟点”的横坐标.
①求实数a的值;
②直接写出另外两个“兄弟点”的横坐标是_______、_______;
(3)若函数$y_{1}=|x - m|$(m为常数)与$y_{2}=-\frac{2}{x}$互为“兄弟函数”,三个“兄弟点”的横坐标分别为$x_{1}$、$x_{2}$、$x_{3}$,且$x_{1}<x_{2}<x_{3}$,求$(x_{2}+x_{3}-2x_{1})^{2}$的取值范围.
(1)下列三个函数①$y = x + 1$;②$y = -\frac{3}{x}$;③$y = -x^{2}+1$,其中与二次函数$y = 2x^{2}-4x - 3$互为“兄弟函数”的是_______(填写序号).
(2)若函数$y_{1}=ax^{2}-5x + 2(a\neq0)$与$y_{2}=-\frac{1}{x}$互为“兄弟函数”,x = 1是其中一个“兄弟点”的横坐标.
①求实数a的值;
②直接写出另外两个“兄弟点”的横坐标是_______、_______;
(3)若函数$y_{1}=|x - m|$(m为常数)与$y_{2}=-\frac{2}{x}$互为“兄弟函数”,三个“兄弟点”的横坐标分别为$x_{1}$、$x_{2}$、$x_{3}$,且$x_{1}<x_{2}<x_{3}$,求$(x_{2}+x_{3}-2x_{1})^{2}$的取值范围.
答案:
(1)② [解析]由图
(1)可知,与二次函数y = 2x² - 4x - 3有3个交点的是y = -$\frac{3}{x}$,
∴与二次函数y = 2x² - 4x - 3互为“兄弟函数”的是②.

(2)①把x = 1代入$y_2 = -\frac{1}{x}$得y = -1,把x = 1,y = -1代入函数$y_1 = ax² - 5x + 2$(a≠0),得a = 2.
②$\frac{3 - \sqrt{17}}{4}$,$\frac{3 + \sqrt{17}}{4}$ [解析]
∵$2x² - 5x + 2 = -\frac{1}{x}$,
∴$2x³ - 5x² + 2x + 1 = 0$,
∴$2x³ - 2x² - 2x² + 2x - x² + 1 = 0$,
∴$(2x³ - 2x²)-(2x² - 2x)-(x² - 1)=0$,
∴$2x²(x - 1)-2x(x - 1)-(x + 1)(x - 1)=0$,
∴$(x - 1)(2x² - 2x - x - 1)=0$,
∴$2x² - 3x - 1 = 0$,
∴$x=\frac{3 - \sqrt{17}}{4}$或$x=\frac{3 + \sqrt{17}}{4}$.
(3)由图
(2)可知,$x_1$满足方程 - x + m = -$\frac{2}{x}$,即$x_1² - mx_1 = 2$,$x_2$、$x_3$满足方程x - m = -$\frac{2}{x}$,即$x_2$、$x_3$是方程$x² - mx + 2 = 0$的两个根,
∴$\Delta = m² - 8>0$,即$m²>8$,$x_2 + x_3 = m$,
∴$(x_2 + x_3 - 2x_1)²=(m - 2x_1)² = m² - 4mx_1 + 4x_1² = m² + 4(x_1² - mx_1)=m² + 8>16$.

思路引导 本题在新定义形式下考查了一次函数、反比例函数、二次函数的图像与性质,图像交点与方程的关系. 解三次方程$2x³ - 5x² + 2x + 1 = 0$时用因式分解法,关键是知道左边一定有因式(x - 1). 第
(3)问利用数形结合,对函数$y_1 = |x - m|$进行分段.
(1)② [解析]由图
(1)可知,与二次函数y = 2x² - 4x - 3有3个交点的是y = -$\frac{3}{x}$,
∴与二次函数y = 2x² - 4x - 3互为“兄弟函数”的是②.

(2)①把x = 1代入$y_2 = -\frac{1}{x}$得y = -1,把x = 1,y = -1代入函数$y_1 = ax² - 5x + 2$(a≠0),得a = 2.
②$\frac{3 - \sqrt{17}}{4}$,$\frac{3 + \sqrt{17}}{4}$ [解析]
∵$2x² - 5x + 2 = -\frac{1}{x}$,
∴$2x³ - 5x² + 2x + 1 = 0$,
∴$2x³ - 2x² - 2x² + 2x - x² + 1 = 0$,
∴$(2x³ - 2x²)-(2x² - 2x)-(x² - 1)=0$,
∴$2x²(x - 1)-2x(x - 1)-(x + 1)(x - 1)=0$,
∴$(x - 1)(2x² - 2x - x - 1)=0$,
∴$2x² - 3x - 1 = 0$,
∴$x=\frac{3 - \sqrt{17}}{4}$或$x=\frac{3 + \sqrt{17}}{4}$.
(3)由图
(2)可知,$x_1$满足方程 - x + m = -$\frac{2}{x}$,即$x_1² - mx_1 = 2$,$x_2$、$x_3$满足方程x - m = -$\frac{2}{x}$,即$x_2$、$x_3$是方程$x² - mx + 2 = 0$的两个根,
∴$\Delta = m² - 8>0$,即$m²>8$,$x_2 + x_3 = m$,
∴$(x_2 + x_3 - 2x_1)²=(m - 2x_1)² = m² - 4mx_1 + 4x_1² = m² + 4(x_1² - mx_1)=m² + 8>16$.

思路引导 本题在新定义形式下考查了一次函数、反比例函数、二次函数的图像与性质,图像交点与方程的关系. 解三次方程$2x³ - 5x² + 2x + 1 = 0$时用因式分解法,关键是知道左边一定有因式(x - 1). 第
(3)问利用数形结合,对函数$y_1 = |x - m|$进行分段.
查看更多完整答案,请扫码查看


