《2025年单元双测全优测评卷九年级数学下册苏科版》

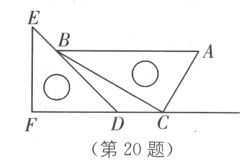
20.(6分)在一次数学活动课上，数学老师在同一平面内将一副直角三角板按如图位置摆放，点C在FD的延长线上，AB//CF，∠F = ∠ACB = 90°，∠E = 45°，∠A = 60°，AC = 10，求CD的长.

答案：
如图，过点B作BM⊥FD于点M.
在△ACB中，∠ACB = 90°，∠A = 60°，AC = 10，
∴∠ABC = 30°，BC = AC·tan 60° = 10$\sqrt{3}$.
∵AB//CF，
∴∠BCM = ∠ABC = 30°.
∴BM = BC·sin 30° = 10$\sqrt{3}$×$\frac{1}{2}$ = 5$\sqrt{3}$，
CM = BC·cos 30° = 10$\sqrt{3}$×$\frac{\sqrt{3}}{2}$ = 15.
在△EFD中，∠F = 90°，∠E = 45°，
∴∠EDF = 45°，
∴MD = BM = 5$\sqrt{3}$，
∴CD = CM - MD = 15 - 5$\sqrt{3}$.

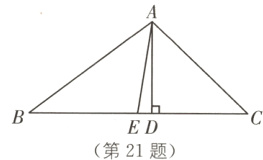
21.(6分)(2024·浙江中考)如图，在△ABC中，AD⊥BC，AE是边BC上的中线，AB = 10，AD = 6，tan∠ACB = 1.
(1)求BC的长；
(2)求sin∠DAE的值.

答案：
(1)
∵AD⊥BC，AB = 10，AD = 6，
∴BD = $\sqrt{AB^{2}-AD^{2}}$ = $\sqrt{10^{2}-6^{2}}$ = 8.
∵tan∠ACB = 1，
∴CD = AD = 6，
∴BC = BD + CD = 8 + 6 = 14.
(2)
∵AE是BC边上的中线，
∴CE = $\frac{1}{2}$BC = 7，
∴DE = CE - CD = 7 - 6 = 1.
∵AD⊥BC，
∴AE = $\sqrt{AD^{2}+DE^{2}}$ = $\sqrt{6^{2}+1^{2}}$ = $\sqrt{37}$，
∴sin∠DAE = $\frac{DE}{AE}$ = $\frac{1}{\sqrt{37}}$ = $\frac{\sqrt{37}}{37}$.

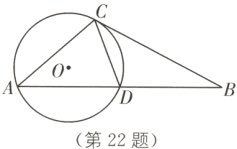
22.(6分)(2024·苏州中考)如图，△ABC中，AB = 4$\sqrt{2}$，D为AB中点，∠BAC = ∠BCD，cos∠ADC = $\frac{\sqrt{2}}{4}$，⊙O是△ACD的外接圆.
(1)求BC的长；
(2)求⊙O的半径.

答案：

(1)
∵∠BAC = ∠BCD，∠B = ∠B，
∴△BAC∽△BCD，
∴$\frac{BC}{BD}$ = $\frac{BA}{BC}$.
∵AB = 4$\sqrt{2}$，D为AB中点，
∴BD = AD = 2$\sqrt{2}$，
∴BC² = 16，
∴BC = 4.
(2)如图，过点A作AE⊥CD于点E，连接CO，并延长交⊙O于F，连接AF，

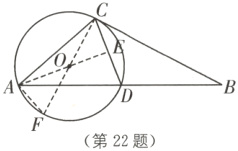
∵在Rt△AED中，cos∠CDA = $\frac{DE}{AD}$ = $\frac{\sqrt{2}}{4}$，AD = 2$\sqrt{2}$，
∴DE = 1，
∴AE = $\sqrt{AD^{2}-DE^{2}}$ = $\sqrt{7}$.
∵△BAC∽△BCD，
∴$\frac{AC}{CD}$ = $\frac{AB}{BC}$ = $\sqrt{2}$.
设CD = x，则AC = $\sqrt{2}$x，CE = x - 1，
∵在Rt△ACE中，AC² = CE² + AE²，
∴($\sqrt{2}$x)² = (x - 1)² + ($\sqrt{7}$)²，即x² + 2x - 8 = 0，
解得x = 2或x = -4(舍去)，
∴CD = 2，AC = 2$\sqrt{2}$.
∵∠AFC与∠ADC都是$\overset{\frown}{AC}$所对的圆周角，
∴∠AFC = ∠ADC.
∵CF为⊙O的直径，
∴∠CAF = 90°，
∴sin∠AFC = $\frac{AC}{CF}$ = sin∠CDA = $\frac{AE}{AD}$ = $\frac{\sqrt{14}}{4}$，
∴CF = $\frac{8\sqrt{7}}{7}$，即⊙O的半径为$\frac{4\sqrt{7}}{7}$.